

·ÖÎö Łš1Ł©·ÖÁœÖÖÇéĐÎŁŹąÙ”±”ăPÔÚAEÉÏʱŁŹÈçÍŒ1ÖĐŁŹÓÉĄśAPNĄŚĄśACBżÉÒÔœâŸöÎÊÌ⣏ąÚ”±”ăPÔÚEDÉÏʱŁŹPN=3ŁŹÈçÍŒ2ÖĐÇółöAE+EPŒŽżÉĄą
Łš2Ł©ąÙÈçÍŒ3ÖĐŁŹ”±3ĄÜtĄÜ6ʱŁŹÖŰ”țČż·ÖÍŒĐÎÎȘËıßĐÎPGKNŁŹÈçÍŒ4ÖĐŁŹąÚÈçÍŒ4ÖĐŁŹ”±6ŁŒtĄÜ9ŁŹÖŰ”țČż·ÖÊÇÎć±ßĐÎPGKHDŁŹ·Ö±đÇółöŒŽżÉŁź
Łš3Ł©·ÖÈęÖÖÇĐÏßÌÖÂÛŒŽżÉąÙ”±ĄÏP1GH=90ĄăŁŹąÚ”±ĄÏP1HG=90ĄăŁŹąÛ”±ĄÏGP1H=90ĄăʱŁź
œâŽđ œâŁșŁš1Ł©ąÙ”±”ăPÔÚAEÉÏʱŁŹÈçÍŒ1ÖĐŁŹ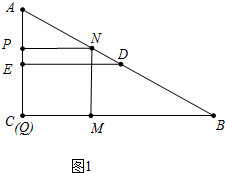
ĄßPNĄÎBCŁŹ
ĄàĄśAPNĄŚĄśACBŁŹ
Ąà$\frac{AP}{AC}$=$\frac{PN}{BC}$ŁŹ
Ąà$\frac{t}{6}$=$\frac{6-t}{12}$ŁŹ
Ąàt=2Ł»
ąÚ”±”ăPÔÚEDÉÏʱŁŹPN=3ŁŹÈçÍŒ2ŁŹ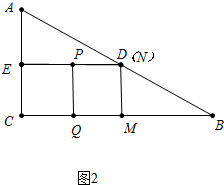
ĄàAE+EP=3+Łš6-3Ł©=6ŁŹ
Ąàt=6Ł»
ŚÛÉÏżÉ”Ăt”ÄÖ”ÎȘ2»ò6ʱŁŹŐę·œĐÎPQMN”Ķ„”ăNÂäÔÚAB±ßÉÏŁ»
Łš2Ł©ÈçÍŒ3ÖĐŁŹ”±3ĄÜtĄÜ6ʱŁŹÖŰ”țČż·ÖÍŒĐÎÎȘËıßĐÎPGKNŁŹ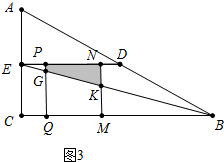
ĄßGQĄÎECŁŹ
Ąà$\frac{GQ}{EC}$=$\frac{BQ}{BC}$ŁŹ
Ąà$\frac{GQ}{3}$=$\frac{15-t}{12}$ŁŹ
ĄàQG=$\frac{1}{4}$Łš15-tŁ©ŁŹPG=3-GQ=$\frac{t-3}{4}$ŁŹÍŹÀíżÉÖȘNK=$\frac{t}{4}$ŁŹ
ĄàS=$\frac{1}{2}$[$\frac{1}{4}$Łšt-3Ł©+$\frac{1}{4}$t]•3=$\frac{3}{4}$t-$\frac{9}{8}$Łź
ÈçÍŒ4ÖĐŁŹ”±6ŁŒtĄÜ9ŁŹÖŰ”țČż·ÖÊÇÎć±ßĐÎPGKHDŁŹ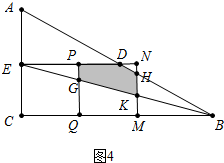
S=SËıßĐÎPGHN-SĄśDNH=-$\frac{1}{4}t$2+$\frac{15}{4}$t-$\frac{81}{8}$Łź
ŚÛÉÏËùÊöŁŹS=$\left\{\begin{array}{l}{\frac{3}{4}t-\frac{9}{8}}&{Łš3ĄÜtĄÜ6Ł©}\\{-\frac{1}{4}{t}^{2}+\frac{15}{4}t-\frac{81}{8}}&{Łš6ŁŒtĄÜ9Ł©}\end{array}\right.$Łź
Łš3Ł©ŽæÔÚŁźÀíÓÉÈçÏÂŁș
čęP1ŚśP1SĄÍACÓÚSŁŹP1RĄÍDEÓÚRŁŹ
ĄßĄÏP1QS=60ĄăŁŹP1Q=3ŁŹ
ĄàP1S=RE=$\frac{3\sqrt{3}}{2}$ŁŹQS=$\frac{3}{2}$ŁŹ
ĄàP1R=SE=$\frac{3}{2}$Łź8·Ö
ąÙ”±ĄÏP1GH=90ĄăʱŁŹÈçÍŒ5ÖĐŁŹ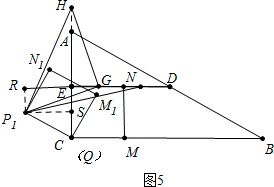

żÉÖ€ĄśP1RGĄŐĄśGEHŁŹ
ÔòEG=P1R=$\frac{3}{2}$Ł»ÈçÍŒ6ÖĐŁŹÍŹÀíżÉ”ĂEG=P1R=$\frac{3}{2}$Łź
ąÚ”±ĄÏP1HG=90ĄăʱŁŹÈçÍŒ7ÖĐŁŹ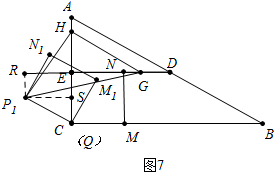
żÉÖ€ĄśP1SHĄŐĄśHEGŁŹ
ĄàEH=P1S=$\frac{3\sqrt{3}}{2}$ŁŹEG=SHŁŹ
ĄàEG=EH+SE=$\frac{3\sqrt{3}}{2}$+$\frac{3}{2}$ŁŹ
»òÈçÍŒ8ÖĐŁŹEG=EH-SE=$\frac{3\sqrt{3}}{2}$-$\frac{3}{2}$Ł»
ąÛ”±ĄÏGP1H=90ĄăʱŁŹ
ĄßP1SĄÙP1RŁŹĄàĄśP1SHÓ륜P1RGČ»żÉÄÜÈ«”ÈŁź
ĄàP1HĄÙP1GŁŹĄàČ»łÉÁąŁź
ŚÛÉÏŁŹEG”Äł€ÎȘ$\frac{3}{2}$»ò$\frac{3\sqrt{3}}{2}$+$\frac{3}{2}$»ò$\frac{3\sqrt{3}}{2}$-$\frac{3}{2}$Łź
”ăÆÀ ±ŸÌâżŒČéÏàËÆĐÎŚÛșÏÌ⥹Őę·œĐΔÄĐÔÖÊĄą”ÈŃüÖ±œÇÈęœÇĐΔÄĐÔÖÊĄąÈ«”ÈÈęœÇĐΔÄĆжšșÍĐÔÖÊĄąÆœĐĐÏß”ÄĐÔÖÊ”ÈÖȘʶŁŹœâÌâ”ÄčŰŒüÊÇѧ»áŐęÈ·»łöÍŒĐÎŁŹŃ§»áÀûÓĂ·Öžî·šÇóĂæ»ęŁŹŃ§»á·ÖÀàÌÖÂÛŚąÒâČ»ÄÜ©œâŁŹÊôÓÚÖĐżŒŃčÖáÌ⣟


 ÔĶÁżìł”Ï”ÁĐŽđ°ž
ÔĶÁżìł”Ï”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | xŁŸ2 | BŁź | xŁŸ-2 | CŁź | -2ŁŒxŁŒ2 | DŁź | xŁŒ-2»ò xŁŸ2 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
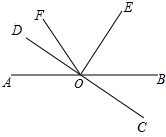 ÈçÍŒŁŹÖ±ÏßABÓëCDÏàœ»ÓÚ”ăOŁŹĄÏAOD=20ĄăŁŹĄÏDOFŁșĄÏFOB=1Łș7ŁŹÉäÏßOEÆœ·ÖĄÏBOFŁŹÔòĄÏEOC=90ĄăŁź
ÈçÍŒŁŹÖ±ÏßABÓëCDÏàœ»ÓÚ”ăOŁŹĄÏAOD=20ĄăŁŹĄÏDOFŁșĄÏFOB=1Łș7ŁŹÉäÏßOEÆœ·ÖĄÏBOFŁŹÔòĄÏEOC=90ĄăŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 3 | BŁź | 2 | CŁź | 1 | DŁź | 0 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com