
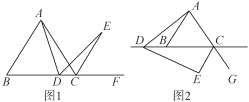
【题目】如图1,△ABC为等边三角形,D为BC上任一点,∠ADE=60°,边DE与∠ACB外角的平分线相交于点E.
(1)求证:AD=DE.
(2)若点D在CB的延长线上,如图2,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;
(2)延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,然后证明△AMD≌△ECD(ASA),根据全等三角形的对应边相等,即可证得.
(1)证明:如图1,在AB上取一点M,使BM=BD,连接MD.
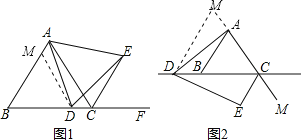
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECF=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠CDE+∠ADE=∠MAD+∠B,
∴∠CDE=∠MAD.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,
 ,
,
∴△AMD≌△DCE(ASA),
∴AD=DE.
(2)答:正确.
证明:延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,
∴∠CDM=∠M=60°,CD=DM,
∵∠ADE=60°,
∴∠ADM=∠EDC,
在△AMD和△DCE中,
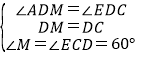 ,
,
∴△AMD≌△ECD(ASA),
∴AD=DE.


科目:初中数学 来源: 题型:
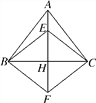
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画 ![]() ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
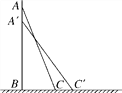
【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: ![]() ≈1.732)
≈1.732)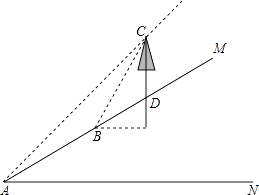
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:在直角三角形中至少有一个角不大于45°.
已知:如图所示,△ABC中,∠C=90°,求证:∠A,∠B中至少有一个不大于45°.
证明:假设__________,则∠A__________45°,∠B______45°. ∴∠A+∠B+∠C>45°+ _______+__________,这与________________________相矛盾. 所以___________不能成立,所以∠A,∠B中至少有一个角不大于45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com