已知一个梯形的四边长分别为1cm、2cm、3cm、4cm,则它的面积为 .
【答案】
分析:首先过点D作DE∥AB交BC于E,易证得四边形ABED是平行四边形,即可得DE=AB,BE=AD,然后利用三角形三边关系分别分析1cm,2cm,3cm,4cm分别是那个边的值,即可确定AD=1cm,AB=2cm,BC=4cm,CD=3cm,然后过点C作CF⊥DE于F,过点D作DH⊥BC于H,利用等腰三角形的性质与勾股定理求得CF的长,又由三角形面积的求解方法,求得梯形的高DH的长,继而求得此梯形面积.
解答: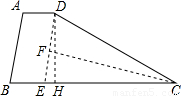
解:如图:过点D作DE∥AB交BC于E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴DE=AB,BE=AD,
若AD=1cm,AB=2cm,BC=3cm,CD=4cm,
则DE=2cm,EC=BC-BE=BC-AD=3-1=2(cm),
∵DE+EC=2+2=4=CD,
∴此时不能组成三角形,既不能组成梯形,
同理可判定:AD=1cm,AB=2cm,BC=4cm,CD=3cm,
过点C作CF⊥DE于F,过点D作DH⊥BC于H,
∵EC=BC-BE=4-1=3(cm),CD=3cm,DE=2cm,
∴CD=CE,
∴DF=EF=

DE=1(cm),
在Rt△CEF中,CF=
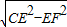
=2
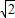
(cm),
∵S
△CDE=

CE•DH=

DE•CF,
∴DH=
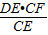
=
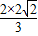
=
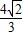
(cm),
∴S
梯形ABCD=

(AD+BC)•DH=

×(1+4)×

=
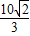
(cm
2).
故答案为:
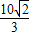
cm
2.
点评:此题考查了梯形的性质,等腰三角形的性质,平行四边形的判定与性质以及勾股定理的应用等知识.此题综合性很强,难度较大,解题的关键是注意分类讨论思想与数形结合思想的应用.

 解:如图:过点D作DE∥AB交BC于E,
解:如图:过点D作DE∥AB交BC于E, DE=1(cm),
DE=1(cm),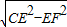 =2
=2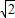 (cm),
(cm), CE•DH=
CE•DH= DE•CF,
DE•CF,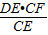 =
=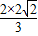 =
=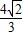 (cm),
(cm), (AD+BC)•DH=
(AD+BC)•DH= ×(1+4)×
×(1+4)× =
=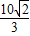 (cm2).
(cm2).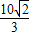 cm2.
cm2.
