
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
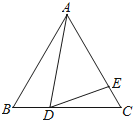
(1)求证:△ABD∽△DCE.
(2)若AB=9cm,BD=3cm,求EC的长.
【答案】(1)见解析;(2)CE=2
【解析】
试题分析:(1)根据等边三角形的性质得到∠B=∠C=60°,AB=BC;等量代换得到∠DAB=∠EDC,根据相似三角形的判定即可得到结论;
(2)根据等边三角形的想在得到AB=BC=9cm,求得CD=6cm,根据相似三角形的性质得到![]() ,代入数据即可得到结论.
,代入数据即可得到结论.
(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC;
∴CD=BC﹣BD=AB﹣3;
∴∠BAD+∠ADB=120°
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE;
(2)∵△ABC是等边三角形,
∴AB=BC=9cm,∵BD=3cm,
∴CD=6cm,
∵△ABD∽△DCE,
∴![]() ,
,
即![]() ,
,
∴CE=2.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
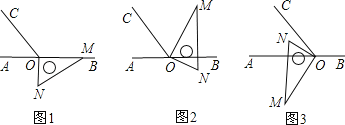
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
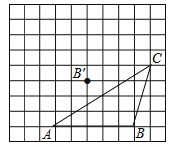
【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,D为BC边上一点,CD=3,过A,C,D三点的⊙O与斜边AB交于点E,连结DE.
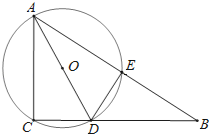
(1)求证:△BDE∽△BAC;
(2)求△ACD外接圆的直径的长;
(3)若AD平分∠CAB,求出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.经过两点有且只有一条直线
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com