
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ-6����B��������A���Ҳ࣬��AB=14������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt(t>O)�룮![]()
��1��д�������ϵ�B��ʾ���� �� ��M��ʾ���� (�ú�t��ʽ�ӱ�ʾ)��
��2������N�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������M��Nͬʱ�������ʵ�M�˶�������ʱ�ϵ�N?
��3����PΪAM���е㣬FΪMB���е㣬��M���˶������У��߶�_PF�ij����Ƿ����仯?���仯����˵�����ɣ������䣬������߶�PF�ij���
���𰸡�
��1��8��-6+5t
��2���⣺ ![]() ��
��![]() ��
��![]() ��
��
�𣺵�M�˶�7��ʱ�ϵ�N
��3���⣺��M���˶������У��߶�PF�ij��Ȳ������仯��
�ٵ���M��AB��ʱ������ͼ��ʾ��![]()
![]() =
= ![]() =
= ![]() ��
��
�ڵ���M��AB�ӳ�����ʱ������ͼ��ʾ��![]()
![]() =
= ![]() =
= ![]()
���������⣺��1���������֪AB=14��OA=6��OB=AB-OA=14-6=8�����Ե�B��ʾ����Ϊ8.��������ɵ�M��ʾΪ-6+5t��![]() (1��A��ʾ����Ϊ-6����B��������A���Ҳ࣬��AB=14 ,�ʸ����߶εĺͲ�ó���B��ʾ������8������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt(t>O)�룬��M��ʾΪ-6+5t��
(1��A��ʾ����Ϊ-6����B��������A���Ҳ࣬��AB=14 ,�ʸ����߶εĺͲ�ó���B��ʾ������8������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt(t>O)�룬��M��ʾΪ-6+5t��
��2��������ʵ��һ�������⣬���ݵ�M��Nͬʱ��������M�ϵ�Nʱ�����M�˶���·��Ϊ5t��N���˶���·��Ϊ3t�����ݵ�M�˶���·��-��N�˶���·��=����֮��ľ��룬�г����̣����ó��𰸣�
��3����M���˶������У��߶�PF�ij��Ȳ������仯�����������������ٵ���M��AB��ʱ�������߶ε��е㶨�弰�߶εĺͲ�ó�P F = P M + F M = ![]() A M +
A M + ![]() B M =
B M = ![]() ( A M + B M ) =
( A M + B M ) = ![]() A B���ڵ���M��AB�ӳ�����ʱ�������߶ε��е㶨�弰�߶εĺͲ�ó�P F = P M F M =
A B���ڵ���M��AB�ӳ�����ʱ�������߶ε��е㶨�弰�߶εĺͲ�ó�P F = P M F M = ![]() A M
A M ![]() B M =
B M = ![]() ( A M B M ) =
( A M B M ) = ![]() A B���Ӷ��ó��𰸡�
A B���Ӷ��ó��𰸡�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
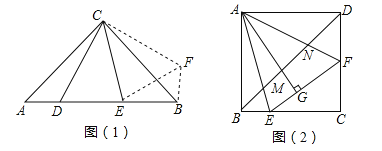
����Ŀ�����⣺��ͼ��1������Rt��ACB�У���ACB=90����AC=CB����DCE=45������̽��AD��DE��EB����ĵ�����ϵ��
[̽������]
С��ͬѧ����ͼ�α任������CAD�Ƶ�C��ʱ����ת90���õ���CBH������EH������֪��������EBH=90������ECH=��ECB+��BCH=��ECB+��ACD=45�������ݡ��߽DZߡ�����֤��CEH�� ����EH=ED��
��Rt��HBE�У��� �������ɵ�BH2+EB2=EH2����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ�� ��
[ʵ������]
��1����ͼ��2������������ABCD�У���AEF�Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ�����EAF�Ķ�����
��2���ڣ�1�������£�����BD���ֱ�AE��AF�ڵ�M��N����BE=2��DF=3��BM=2![]() ������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij���
������С��ͬѧ̽���Ľ��ۣ��������εı߳���MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD= ![]() AB=
AB= ![]() CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���
CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijѧУȫ���ְ�������Ƶ���ֲ�ֱ��ͼ��ÿ�����������Сֵ�����������ֵ��������ͼ���ṩ����Ϣ������˵���д�����ǣ� �� 
A.��ѧУ��ְ����������50��
B.��һ��������40��x��42С��Ľ�ְ������ռ��ѧУȫ���ְ����������20%
C.��ְ���������λ��һ������40��x��42��һ��
D.��ְ�����������һ����38��x��40��һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լˮ��Դ��ij�������վ����ͥ����ˮ��ʵ�н���ˮ�ۣ�ˮ�۷ֵ��������ƻ�ʹ��һ�����ڶ����͵�������ˮ�۷ֱ�ȫ�о����ͥ��80%��15%��5%��Ϊ����ȷ������֮��Ľ��ޣ��������˸���5�����ͥ��һ�������ˮ������λ��m3����������ͳ��ͼ����ͼ��ʾ�������ĸ��ƶϣ�������
������ˮ��������180m3�ĸ��о����ͥ����һ��ˮ�۽��ѣ�
������ˮ������240m3�ĸ��о����ͥ��������ˮ�۽��ѣ�
�۸��о����ͥ����ˮ������λ����150��180֮�䣻
�ܸ��о����ͥ����ˮ����ƽ����������180��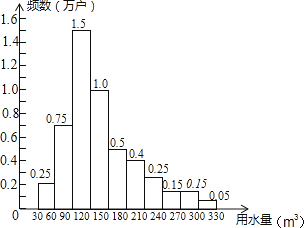
A.�٢�
B.�٢�
C.�ڢ�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����������߶���һ���ܽ������ηֳ������ȵ������ֵ��ǣ� ��
A.��ƽ����
B.���
C.��
D.����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com