
【题目】在△ABC中,∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数
科目:初中数学 来源: 题型:
【题目】请把下列证明过程补充完整(括号内填写相应的理由)
已知:如图,点E在BC延长线上,AE交CD于点F,AD∥BC,∠1=∠2,∠3=
∠4,求证:AB∥CD.

证明:∵AD∥BC(已知)
∴∠3=∠______( )
又∵∠3=∠4(已知)
∴∠4=∠______( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式性质)
即∠BAF=∠_______
∴∠4=∠________( )
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
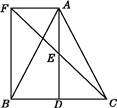
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(1,0),点
的坐标为(1,0),点![]() 的横坐标为2,将点
的横坐标为2,将点 ![]() 绕点P旋转,使它的对应点
绕点P旋转,使它的对应点![]() 恰好落在
恰好落在![]() 轴上(不与
轴上(不与![]() 点重合);再将点
点重合);再将点![]() 绕点O逆时针旋转90°得到点
绕点O逆时针旋转90°得到点![]() .
.
(1)直接写出点![]() 和点C的坐标;
和点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
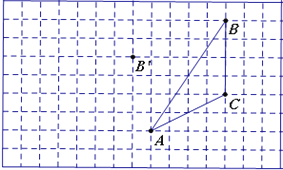
(1) 补全△A′B′C′;
(2) 根据下列条件,利用网格点和直尺画图:
画出△ABC中:
①AC边上的中线BD;
②AC边上的高线BE;
(3)写出△ABD的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
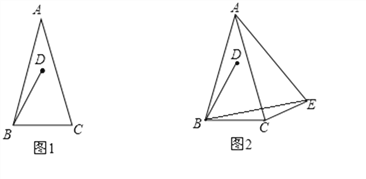
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),点D在△ABC内,且BD=BC,∠DBC=60°.
(1)如图1, 连接AD,直接写出∠ABD的度数(用含α的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
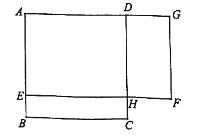
【题目】如图, ![]() 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形![]() 的形状,其中点
的形状,其中点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 设
设![]() 的长为
的长为![]() 米,改造后苗圃
米,改造后苗圃![]() 的面积为
的面积为![]() 平方米.
平方米.
(1) ![]() 与
与![]() 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃![]() 的面积与原正方形苗圃
的面积与原正方形苗圃![]() 的面积相等,请问此时
的面积相等,请问此时![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com