
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6cm,点D是线段AB上一动点,将线段CD绕点C逆时针旋转50°至CD′,连接BD′.设AD为xcm,BD′为ycm.
小夏根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
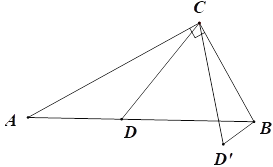
下面是小夏的探究过程,请补充完整.
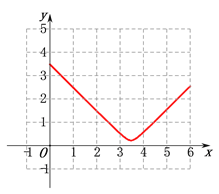
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 1 | 2 | 3 | 3.5 | 4 | 5 | 6 |
| 3.5 | 1.5 | 0.5 | 0.2 | 0.6 | 1.5 | 2.5 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当BD=BD'时,线段AD的长度约为_________![]() .
.
【答案】(1)2.5;(2)见解析;(3)4.7
【解析】
(1)观察、分析表格中的数据可得:点(0,3.5),(2,1.5),(3,0.5)三个点在同一直线上,求出过这三点的直线的解析式,即可求得当x=1时的y的对应值;
(2)在所给方格纸中建立平面直角坐标系,然后根据表格中所给数据描出各点,并把各点用“平滑的曲线”连接起来即可;
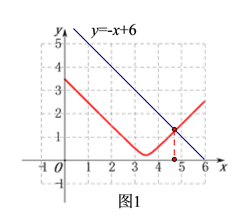
(3)由题意可知,当BD=BD′时,6-x=y,即y=-x+6,在(2)中所得图象中画出直线y=-x+6的图象如下图1所示,则两个函数图象交点的横坐标为所求的x的值.
(1)设过点(2,1.5)和(3,0.5)的直线的解析式为y=kx+b,由此可得:
![]() ,解得:
,解得:![]() ,
,
∴过点(2,1.5)和(3,0.5)的直线的解析式为:y=-x+3.5,
∵当x=0时,y=3.5,
∴点(0,3.5)也在该直线上,
由此可知y与x的函数关系在![]() 的范围内是:y=-x+3.5,
的范围内是:y=-x+3.5,
∴当x=1时,y=-1+3.5=2.5,
∴将y=2.5填入表格的空格处即可;
(2)在方格纸中建立如下图所示的坐标系,然后按表格中所给数据描出各点,再将各点顺次连接,即可得到如下图所示的函数图象:
(3)∵BD=AB-AD=6-x,BD′=y,
∴当BD=BD′时,6-x=y,即:y=-x+6,
在(2)所得的函数坐标系中画出直线y=-x+6的图象(如图1所示),则两个函数图象的交点的横坐标即为BD=BD′时的x的值,
由下图可得:两函数图象交点的横坐标约为:4.7,
∴当BD=BD′时,x=4.7,即此时BD的长约为4.7cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在![]() 中,若
中,若![]() ,则
,则![]() 是“和谐三角形”.
是“和谐三角形”.

(1)等边三角形一定是“和谐三角形”,是______命题(填“真”或“假”).
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() .
.
(3)如图2,在等边三角形![]() 的边
的边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的高,若
的高,若![]() 是“和谐三角形”,且
是“和谐三角形”,且![]() .
.

①求证:![]() .
.
②连结![]() ,若
,若![]() ,那么线段
,那么线段![]() ,
,![]() ,
,![]() 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图,下列说法中,错误的是
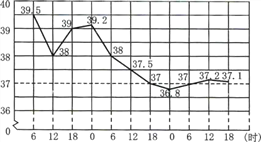
①护士每隔6小时给病人量一次体温;
②这个病人的体温最高是39.5摄氏度,最低36.8摄氏度;
③他的体温在4月9日18时到4月10日18时比较稳定;
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
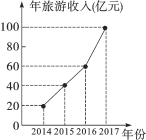
【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
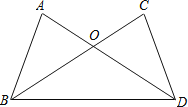
【题目】(1)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
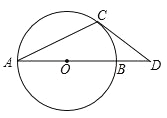
(2)如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD=![]() ,求∠BAC的度数.
,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:(假设行车过程没有停车等时,且平均车速为0.5千米/分钟)
华夏专车 | 神州专车 | |
里程费 | 1.8元/千米 | 2元/千米 |
时长费 | 0.3元/分钟 | 0.6元/分钟 |
远途费 | 0.8元/千米产(超过7千米部分) | 无 |
起步价 | 无 | 10元 |
华夏专车:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出的部分按每千米加收0.8元. 神州专车:车费由里程费、时长费、起步价三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;起步价与行车距离无关. | ||
(1)小明在该地区出差,乘车距离为10千米,如果小明使用华夏专车,需要支付的打车费用为 元;
(2)小强在该地区从甲地乘坐神州专车到乙地,一共花费42元,求甲乙两地距离是多少千米?
(3)神州专车为了和华夏专车竞争客户,分别推出了优惠方式,华夏专车对于乘车路程在7千米以上(含7千米)的客户每次收费立减9元;神州打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com