
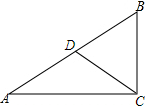
 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,若∠A=30°,CD=2,求AC的长.
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,若∠A=30°,CD=2,求AC的长. 分析 根据直角三角形斜边上的中线等于斜边的一半求出AB,根据直角三角形30°角所对的直角边等于斜边的一半求出BC,然后利用勾股定理列式计算即可得解.
解答 解:∵∠ACB=90°,D为AB的中点,
∴AB=2CD=2×2=4,
∵∠A=30°,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
在Rt△ABC中,根据勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半,直角三角形30°角所对的直角边等于斜边的一半的性质,以及勾股定理,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.
已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 2017年 月 农历丙申(猴)年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com