
【题目】已知,△ABC是等边三角形,四边形ACFE是平行四边形,AE=BC.
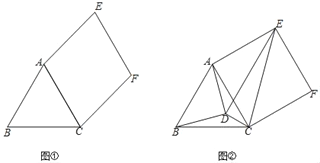
(1)如图①,求证:ACFE是菱形;
(2)如图②,点D是△ABC内一点,且∠ADB=90°,∠EDC=90°,∠ABD=∠ACE.求证:ACFE是正方形.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)由题意直接可证
(2)由题意可证△ABD≌△AGC 可证AG=AD,∠BAD=∠CAG可得△ADG是等边三角形,且根据直角三角形斜边上中线等于斜边一半,可得DG=EG=CG=AG. 即可证得结论.
证明:(1)∵△ABC是等边三角形,
∴AC=BC.
∵AE=BC,
∴AC=AE.
∵四边形ACFE是平行四边形,
∴ACFE是菱形.
(2)证明:连接AF交CE于点G,连接DG
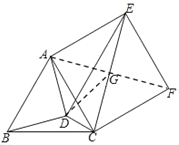
由(1)得ACFE是菱形,
∴∠AGC=90°,∠GAC=∠EAG,CG=EG.AG=GF
∵∠ADB=90°,
∴∠ADB=∠AGC.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
在△ABD和△ACG中,
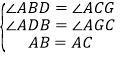
∴△ABD≌△ACG.
∴AD=AG,∠BAD=∠CAG.
∴∠BAD+∠DAC=∠CAG+∠DAC.
即∠BAC=∠DAG.
∵∠BAC=60°,
∴∠DAG=60°.
∵AD=AG,
∴△DAG是等边三角形.
∴AG=DG.
∵∠EDC=90°,CG=EG,
在Rt△EDC中,
有![]() .
.
∵AG=DG,
∴AG=CG.
∴AF=CE
又∵ACFE是菱形,
∴ACFE是正方形.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是轴对称图形,且直线AC是否对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是( )

A. ①②③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.
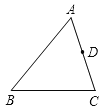
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(不要求写作法)如图,在 10×10 的方格纸中,有一个格点四边形 ABCD(即四边形的顶点都在格点上)。①在给出的方格纸中,画出四边形 ABCD 向下平移 5 格后的四边形 A![]() B
B![]() C
C![]() D
D![]() ;②在给出的方格纸中,画出四边形 ABCD 关于直线 l 对称的图形 A
;②在给出的方格纸中,画出四边形 ABCD 关于直线 l 对称的图形 A![]() B
B![]() C
C![]() D
D![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
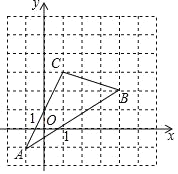
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标;
(2)求出△ABC的面积S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com