
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
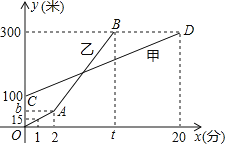
【题目】甲乙两人同时登山,甲乙两人距地面的高度![]() (米
(米![]() 与登山时间
与登山时间![]() (分
(分![]() 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米![]() 分钟,乙在
分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 米;
为 米;
(2)直接写出甲距地面高度![]() (米
(米![]() 和
和![]() (分
(分![]() 之间的函数关系式;
之间的函数关系式;
(3)若乙提速后,乙的速度是甲登山速度的3倍.请问登山多长时间时,乙追上了甲,此时乙距![]() 地的高度为多少米?
地的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
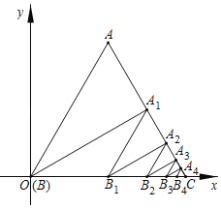
【题目】如图,等边三角形ABC的边长为4,顶点B与原点O重合,点C在x轴的正半轴上,过点B作BA1⊥AC于点A1,过点A1作A1B1∥OA,交OC于点B1;过点B1作B1A2⊥AC于点A2,过点A2作A2B2∥OA,交OC于点B2;……,按此规律进行下去,点A2020的纵坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月23日是第23个“世界读书日”,也是江苏省第四个法定的全民阅读日。由市文明办、市全民阅读办、市文广新局等单位联合主办的“2018无锡市第三个全民阅读日”系列活动即将启动。某校围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
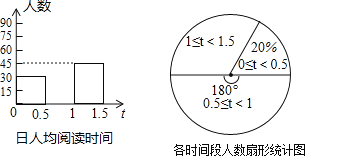
(1)本次抽样调查的样本容量是 .
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角是 度.
(4)根据本次抽样调查,试估计我市12000名初二学生中日人均阅读时间在0.5~1.5小时的多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校七年级小朋友小敏这学期第一周和第二周做家务事的时间统计表,已知小敏每次在做家务事中洗碗的时间相同,扫地的时间也相同.
每周做家务总时间(分) | 洗碗次数 | 扫地的次数 | |
第一周 | 44 | 2 | 3 |
第二周 | 42 | 1 | 4 |
(1)求小敏每次洗碗的时间和扫地的时间各是多少?
(2)为鼓励小敏做家务,小敏的家长准备洗碗一次付12元,扫地一次付8元,总费用不超过100元。请问小敏如何安排洗碗与扫地的次数,既能够让花费的总时间最少,又能够全部拿到100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AC=BC,∠ACB=45°,将三角形ABC沿着AC翻折,点B落在点E处,联结DE,那么![]() 的值为________.
的值为________.
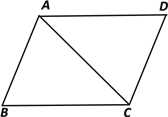
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com