
分析 (1)根据幂的乘方和同底数幂的乘法即可解答本题;
(2)根据同底数幂的乘法即可解答本题;
(3)根据负整数指数幂、零指数幂和整式的减法可以解答本题;
(4)根据积的乘方和合并同类项即可解答本题;
(5)根据互为倒数的乘积为1和幂的乘方可以解答本题.
解答 解:(1)(a2)5•a2
=a10•a2
=a12;
(2)(p-q)3•(p-q)2;
=(p-q)5;
(3)(-2)-2-22÷(3.144)0;
=$\frac{1}{4}-4÷1$
=$\frac{1}{4}-4$
=$-3\frac{3}{4}$;
(4)-x3+(-4x)2x
=-x3+16x3
=15x3;
(5)(-$\frac{5}{12}$)2013×(2$\frac{2}{5}$)2014
=$-(\frac{5}{12})^{2013}×(\frac{12}{5})^{2013}×\frac{12}{5}$
=$-\frac{12}{5}$.
点评 本题考查整式的混合运算、负整数指数幂、零指数幂,解答本题的关键是明确它们各自的计算方法.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
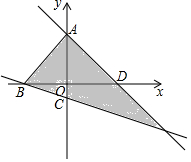
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=90° | C. | ∠1-∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
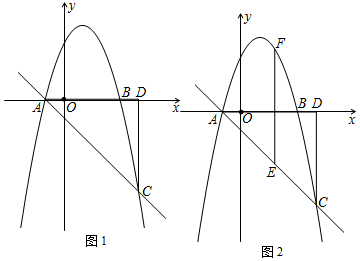
 在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,-1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,-1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
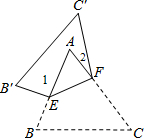 如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为( )
如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为( )| A. | 24° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形的两边长分别为3和4,则斜边长为5 | |
| B. | △ABC中∠A、∠B、∠C的对边分别是a、b、c,如果(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 菱形的对角线相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com