
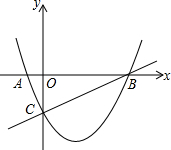
 ��ͼ����֪������y=ax2-$\frac{3}{2}$x+c��x���ཻ��A��B���㣬����ֱ��y=x-2����B��C���㣬���е�C��ֱ��y=$\frac{1}{2}$x-2��y��Ľ��㣬����AC��
��ͼ����֪������y=ax2-$\frac{3}{2}$x+c��x���ཻ��A��B���㣬����ֱ��y=x-2����B��C���㣬���е�C��ֱ��y=$\frac{1}{2}$x-2��y��Ľ��㣬����AC������ ��1�����ô���ϵ����������ת��Ϊ�����鼴�ɽ�����⣮
��2�����ݹ��ɶ������涨�������жϣ�
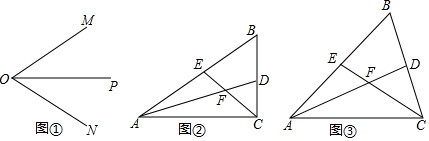
��3������������������ε���������ֵ����ͼ2�У����ı���EFGC�Ǿ���ʱ����ʱ��AGF�ס�ACB�ס�FEB������ͼ3�����ı���EFGD�Ǿ���ʱ����ʱ��CDE�ס�CAB�ס�GAD���ֱ����κ��������ö��κ��������ʼ��ɽ�����⣮
��� ��1���⣺��ֱ��y=$\frac{1}{2}$x-2��x�ᡢy����B��C���㣬
��B��4��0����C��0��-2����
��y=ax2-$\frac{3}{2}$x+c��B��C���㣬
��$\left\{\begin{array}{l}{16a-6+c=0}\\{c=-2}\end{array}\right.$��
��� $\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-2}\end{array}\right.$��
��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��2��֤������ͼ1������AC��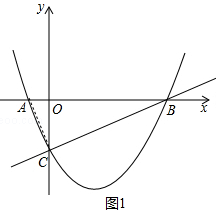
��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��x�����ύ��A�㣬
��A��-1��0����
��Rt��AOC��
��AO=1��OC=2��
��AC=$\sqrt{5}$��
��Rt��BOC��
��BO=4��OC=2��
��BC=2$\sqrt{5}$��
��AB=AO+BO=1+4=5��
��AB2=AC2+BC2��
���ABCΪֱ�������Σ�
��3���⣺��ABC�ڲ��ɽس�������ľ���DEFG�����Ϊ���������£�
����ͼ2�У����ı���EFGC�Ǿ���ʱ����ʱ��AGF�ס�ACB�ס�FEB��
��GC=x��AG=$\sqrt{5}$-x��
��$\frac{AG}{AC}$=$\frac{FG}{CB}$��
��$\frac{\sqrt{5}-x}{\sqrt{5}}$=$\frac{FG}{2\sqrt{5}}$��
��GF=2$\sqrt{5}$-2x��
��S=GC•GF=x•��2$\sqrt{5}$-2x��=-2x2+2$\sqrt{5}$x=-2��x-$\frac{\sqrt{5}}{2}$��2+$\frac{5}{2}$
����x=$\frac{\sqrt{5}}{2}$ʱ��S���Ϊ$\frac{5}{2}$��
����ͼ3�����ı���EFGD�Ǿ���ʱ����ʱ��CDE�ס�CAB�ס�GAD��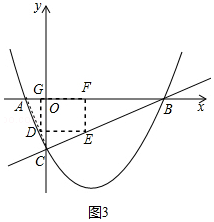
��GD=x��
��$\frac{AD}{AB}$=$\frac{GD}{CB}$��
��$\frac{AD}{5}$=$\frac{x}{2\sqrt{5}}$��
��AD=$\frac{\sqrt{5}}{2}$x��
��CD=CA-AD=$\sqrt{5}$-$\frac{\sqrt{5}}{2}$x��
��$\frac{CD}{AC}$=$\frac{DE}{AB}$��
��$\frac{\sqrt{5}-\frac{\sqrt{5}}{2}x}{\sqrt{5}}$=$\frac{DE}{5}$��
��DE=5-$\frac{5}{2}$x��
��S=GD•DE=x•��5-$\frac{5}{2}$x��=-$\frac{5}{2}$x2+5x=-$\frac{5}{2}$��x-1��2+$\frac{5}{2}$��
��x=1ʱ��S���Ϊ$\frac{5}{2}$��
������������ABC�ڲ��ɽس�������ľ���DEFG�����Ϊ$\frac{5}{2}$��
���� ���⿼����κ������ۺ��⡢���ɶ������涨�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
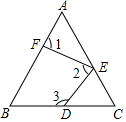 ��ͼ��ֱ��AB��DE��EF ���أ���1�͡�2���ڴ��ǣ�
��ͼ��ֱ��AB��DE��EF ���أ���1�͡�2���ڴ��ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | �� | -2 | -1 | 0 | 1 | 2 | 3 | �� |
| y | �� | 23 | 6 | -3 | -4 | 3 | 18 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
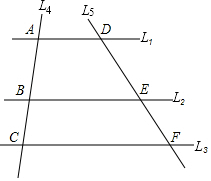 ֱ��L1��L2��L3��ֱ��L4��L1��L2��L3���أ����нصõ������߶ηֱ�ΪAB��BC��L5������һ����L1��L2��L3���ص�ֱ�ߣ����нصõ������߶ηֱ�ΪDE��EF��С��ͨ�������ó�AB��1.89cm��BC��3.80cm��DE��2.02cm����ôEFԼ����4.06cm��
ֱ��L1��L2��L3��ֱ��L4��L1��L2��L3���أ����нصõ������߶ηֱ�ΪAB��BC��L5������һ����L1��L2��L3���ص�ֱ�ߣ����нصõ������߶ηֱ�ΪDE��EF��С��ͨ�������ó�AB��1.89cm��BC��3.80cm��DE��2.02cm����ôEFԼ����4.06cm���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com