
 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、分析 (1)利用点平移的坐标规律,写出A1、B1、C1的坐标,然后即可得到△A1B1C1为所作;
(2)延长BA到A2,使BA2=2BA,则点A2为点A的对应点,同样方法得到C点的对应点C2,点B2与B点重合,则可得到△A2B2C2,然后写出点A2的坐标;
(3)用一个矩形的面积分别减去三个直角三角形的面积可得到△A2B2C2的面积.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,点A2的坐标为(-3,2);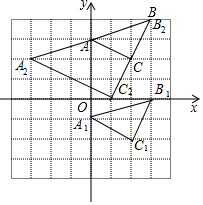
(3)△A2B2C2的面积=6×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×6=10.
故答案为(-3,2),10.
点评 本题考查了作图-位似变化:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | ∠A+∠B=∠C | B. | ∠A=∠B=$\frac{1}{2}$∠C | C. | ∠A=90°-∠B | D. | ∠A=2∠B=3∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com