
【题目】山青养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,统计了它们的质量(单位:kg),并绘制出如下的统计图1和图2.

请根据以上信息解答下列问题:
(1)图1中m的值为 ;
(2)统计的这组数据的众数是 ;中位数是 ;
(3)求出这组数据的平均数,并估计这2500只鸡的总质量约为多少kg.
【答案】(1)28;(2)1.8kg,1.5kg;(3)平均数是1.52kg,总质量约为3800kg.
【解析】
(1)根据各种质量的百分比之和为1可得m的值;
(2)根据众数、中位数、加权平均数的定义计算即可;
(3)根据平均数的计算公式求出这组数据的平均数,再乘以总只数即可得出鸡的总质量.
(1)图①中m的值为100﹣(32+8+10+22)=28,
故答案为:28;
(2)∵1.8kg出现的次数最多,
∴众数为1.8kg,
把这些数从小到大排列,则中位数为![]() =1.5(kg);
=1.5(kg);
故答案为:1.8kg,1.5kg;
(3)这组数据的平均数是:
![]() ×(5×1+11×1.2+14×1.5+16×1.8+4×2),
×(5×1+11×1.2+14×1.5+16×1.8+4×2),
=![]() (5+13.2+21+28.8+8),
(5+13.2+21+28.8+8),
=1.52(kg),
∴2500只鸡的总质量约为:1.52×2500=3800(kg),
所以这组数据的平均数是1.52kg,2500只鸡的总质量约为3800kg.


科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
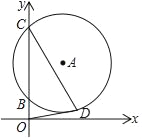
【题目】如图,以点A(1,![]() )为圆心的⊙A交y轴正半轴于B,C两点,且OC=
)为圆心的⊙A交y轴正半轴于B,C两点,且OC=![]() +1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )
+1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )
A. ![]() ﹣1 B. 2
﹣1 B. 2![]() C. 2
C. 2![]() D.
D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
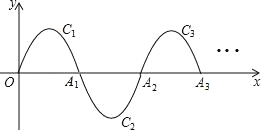
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
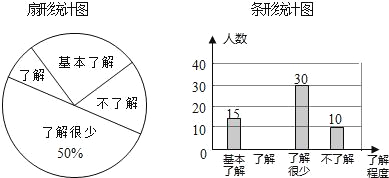
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
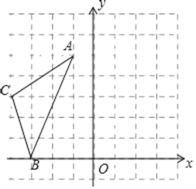
【题目】如图,在平面直角坐标中,已知A(﹣1,5),B(﹣3,0),C(﹣4,3)
(1)在图中作出△ABC关于y轴对称的图形△A′B′C′;
(2)如果线段AB的中点是P(﹣2,m),线段A'B'的中点是(n﹣1,2.5).求m+n的值.
(3)求△A'B'C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
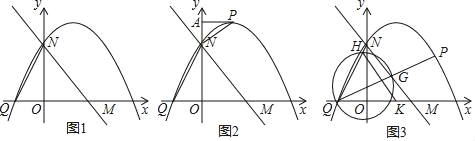
【题目】已知在平面直角坐标系xOy中,O是坐标原点,如图1,直角三角板△MON中,OM=ON=![]() ,OQ=1,直线l过点N和点N,抛物线y=ax2+
,OQ=1,直线l过点N和点N,抛物线y=ax2+![]() x+c过点Q和点N.
x+c过点Q和点N.
(1)求出该抛物线的解析式;
(2)已知点P是抛物线y=ax2+![]() x+c上的一个动点.
x+c上的一个动点.
①初步尝试
若点P在y轴右侧的该抛物线上,如图2,过点P作PA⊥y轴于点A,问:是否存在点P,使得以N、P、A为顶点的三角形与△ONQ相似.若存在,求出点P的坐标,若不存在,请说明理由;
②深入探究
若点P在第一象限的该抛物线上,如图3,连结PQ,与直线MN交于点G,以QG为直径的圆交QN于点H,交x轴于点R,连结HR,求线段HR的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com