
分析 (1)利用勾股定理求出AB的长即可解决问题.
(2)如图1中,设y=2x+b与双曲线y=-$\frac{1}{x}$的交点为A、B.作BC⊥x轴于C,AE⊥BC于E.由AB=$\sqrt{5}$,则AE=1,BE=2,设A(m,-$\frac{1}{m}$),则B(m+1,-$\frac{1}{m}$+2),可得(m+1)(-$\frac{1}{m}$+2)=-1,解得m=$\frac{-1±\sqrt{5}}{2}$,推出A($\frac{-1-\sqrt{5}}{2}$,$\frac{\sqrt{5}-1}{2}$)或($\frac{-1+\sqrt{5}}{2}$,$\frac{-1-\sqrt{5}}{2}$),再利用待定系数法即可解决问题.
(3)如图2中,设P(x1,y1),Q(x2,y2),由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+mx-1}\end{array}\right.$消去y得到,x2+(m-1)x-1=0,可得x1+x2=1-m,x1x2=-1,y1=x1-2,y2=x2-2,推出y1+y2=m-5,y1y2=5-2m,
求出PQ,利用二次函数的性质,推出m=1时,非凡距离PQ的值最小,求出点P、Q的坐标,即可解决问题.
解答 解:(1)对于直线y=x+4,令x=0得y=4,令y=0得x=-4,
不妨设A(0,4),B(-4,0),
∴OA=OB=4,
∴直线l与折线AOB的非凡距离=AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
(2)如图1中,设y=2x+b与双曲线y=-$\frac{1}{x}$的交点为A、B.作BC⊥x轴于C,AE⊥BC于E.
∵AB=$\sqrt{5}$,则AE=1,BE=2,设A(m,-$\frac{1}{m}$),则B(m+1,-$\frac{1}{m}$+2),
∴(m+1)(-$\frac{1}{m}$+2)=-1,
解得m=$\frac{-1±\sqrt{5}}{2}$,
∴A($\frac{-1-\sqrt{5}}{2}$,$\frac{\sqrt{5}-1}{2}$)或($\frac{-1+\sqrt{5}}{2}$,$\frac{-1-\sqrt{5}}{2}$),
把点A坐标代入y=2x+b中,可得b=$\frac{3\sqrt{5}+1}{2}$或$\frac{1-3\sqrt{5}}{2}$.
(3)如图2中,设P(x1,y1),Q(x2,y2),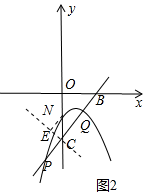
由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+mx-1}\end{array}\right.$消去y得到,x2+(m-1)x-1=0,
∴x1+x2=1-m,x1x2=-1,y1=x1-2,y2=x2-2,
∴y1+y2=m-5,y1y2=5-2m,
∴PQ=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}+({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(1-m)^{2}+4+(m-5)^{2}-4(5-2m)}$=$\sqrt{2(m-1)^{2}+8}$,
∵2>0,
∴m=1时,非凡距离PQ的值最小,
由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+x-1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$,
不妨设P(-1,-3),Q(1,-1),设线段PQ与y轴的解得为C,则C(0,-2),
∴PC=CQ=$\sqrt{2}$,
∵⊙M经过P、Q两点,
∴点M在线段PQ的中垂线EC上,作NE⊥CE于E,
∵OC=OB=2,
∴∠OCB=∠ECN=45°,
∵N(0,-1),
∴ON=1,CN=1,
在Rt△NEC中,NE=CN•cos45°=$\frac{\sqrt{2}}{2}$,
∴点N到⊙M的圆心M的距离的最小值为$\frac{\sqrt{2}}{2}$.
点评 本题考查二次函数综合题、一次函数的应用、反比例函数的应用、一元二次方程的根与系数关系等知识,解题的关键是理解题意,学会利用参数解决问题,用转化的思想思考问题,学会构建二次函数解决最值问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.296868×104 | B. | 2.96868×105 | C. | 2.96868×106 | D. | 29.6868×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
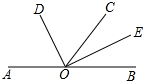 填空,完成下列说理过程:
填空,完成下列说理过程:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
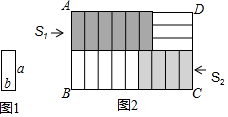 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )| A. | 5b=2a | B. | 2b=a | C. | 3b=a | D. | 5b=3a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015年我市七年级学生是总体 | |
| B. | 样本容量是1000 | |
| C. | 1000名七年级学生是总体的一个样本 | |
| D. | 每一名七年级学生是个体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com