练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将等边△ABC绕顶点A按顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数为_______.

    60° 【解析】∵将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F， ∴旋转角为60°，E，F是对应点， 则∠EAF的度数为：60°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

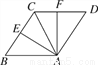
    科目：初中数学 来源：甘肃省平凉市2017-2018学年八年级（上）期中数学试卷 题型：填空题

    已知等腰三角形两边长是4cm和9cm，则它的周长是________．

    22cm 【解析】分析：本题考查的是等腰三角形的两个腰相等，组成三角形的三边关系解决即可. 解析：等腰三角形三边可能是：4、4、9，4、9、9；∵4、4、9不能组成三角形，故周长为4+9+9=22（cm）. 故答案为22cm.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第3章 一元一次方程 单元测试卷 题型：解答题

    （15分）解下列方程：

    （1）4x－3（12－x）＝6x－2（8－x）；

    （2）；

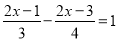    （3）．

    （1）x＝－20；（2）x＝；（3）x＝3． 【解析】试题分析：（1）先去括号，再移项，化系数为1，从而得到方程的解； （2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解； （3）去括号后合并同类项即可． 试题解析： 【解析】 （1）去括号得：4x-36+3x=6x-16+2x，移项合并同类项得：﹣x=20，系数化为1得：x...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第3章 一元一次方程 单元测试卷 题型：单选题

    小马虎在做作业，不小心将方程中的一个常数污染了，被污染的方程是2（x－3）－■＝x＋1，怎么办呢？他想了想便翻看书后的答案，方程的解是x＝9，请问这个被污染的常数是（　　）

    A. 1 B. 2 C. 3 D. 4

    B 【解析】【解析】 设被污染的数字为y． 将x=9代入得：2×6﹣y=10． 解得：y=2． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：解答题

    如图，已知四边形ABCD，画四边形A1B1C1D1，使它与四边形ABCD关于C点中心对称．

    见解析 【解析】试题分析：分别画出A、B、C、D各点关于点C的对称点，然后顺次连接即可． 【解析】 四边形A1B1C1D1如图所示.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：单选题

    如图所示的两个三角形是经过何种变换得到的(　　)

    A. 旋转 B. 旋转和平移 C. 轴对称 D. 平移和轴对称

    D 【解析】试题解析： 沿平移个长度单位，然后作关于 对称的图形即可得到 故两个三角形是经过平移和轴对称变换得到的. 答案：D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：单选题

    如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（　　）

    A. （，1） B. （1，﹣） C. （2，﹣2） D. （2，﹣2）

    B 【解析】试题分析：根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD，连接OP，OQ，过Q作QM⊥y轴，由旋转的性质得到∠POQ=120°，根据AP=BP=OP=2，得到∠AOP度数，进而求出∠MOQ度数为30°，在直角三角形OMQ中求出MQ=1，OM=，即可确定出Q的坐标为（1，﹣），故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第25章 概率初步 单元测试卷 题型：填空题

    用“必然事件”“不可能事件”“随机事件”填空：(1)明天要下雨___________；(2)小明身高3.5m____________；(3)两直线平行，同位角相等___________．

    随机事件 , 不可能事件, 必然事件 【解析】随机事件是可能发生，也可能不发生的事件，由此可得明天要下雨是随机事件；必然事件是一定能够发生的事件，由此可得两直线平行，同位角相等是必然事件；不可能事件是一定不能够发生的事件，由此可得小明身高3.5m是不可能事件.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：解答题

    已知平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F．求证：CF2=GF•EF．

    证明见解析 【解析】试题分析：根据平行四边形的性质，得到平行关系，然后根据平行线分线段成比例可证明. 试题解析：∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD， ∴GF:CF=DF:BF，CF:EF=DF:BF， ∴GF:CF=CF:EF， 即CF2=GF•EF．

    查看答案和解析>>

    同步练习册答案