
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )| A. | 1 | B. | 4-2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$-4 |
分析 在AF上取FG=EF,连接GE,可得△EFG是等腰直角三角形,根据等腰直角三角形的性质可得EG=$\sqrt{2}$EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.
解答 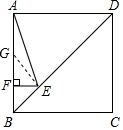 解:如图,在AF上取FG=EF,连接GE,
解:如图,在AF上取FG=EF,连接GE,
∵EF⊥AB,
∴△EFG是等腰直角三角形,
∴EG=$\sqrt{2}$EF,∠EGF=45°,
由三角形的外角性质得,∠BAE+∠AEG=∠EGF,
∵∠BAE=22.5°,∠EGF=45°,
∴∠BAE=∠AEG=22.5°,
∴AG=EG,
在正方形ABCD中,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴BF=EF,
设EF=x,∵AB=AG+FG+BF,
∴4=$\sqrt{2}$x+x+x,
解得x=2(2-$\sqrt{2}$)=4-2$\sqrt{2}$.
故选B.
点评 本题考查了正方形的性质,等腰直角三角形的判定与性质,难点在于作辅助线构造出等腰直角三角形并根据正方形的边长AB列出方程.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
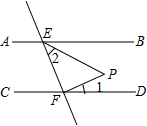 如图,直线AB∥CD,直线EF分别于AB,CD交于点E,F,FP⊥EF于点F,且与∠BEF的平分线交于点P,若∠1=20°,则∠P的度数是55°.
如图,直线AB∥CD,直线EF分别于AB,CD交于点E,F,FP⊥EF于点F,且与∠BEF的平分线交于点P,若∠1=20°,则∠P的度数是55°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,∠A=70°,将?ABCD绕点B顺时针旋转到?A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=( )
如图,在?ABCD中,∠A=70°,将?ABCD绕点B顺时针旋转到?A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥EF,交直线AB于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥EF,交直线AB于点G.若∠1=36°,则∠2的大小是( )| A. | 36° | B. | 54° | C. | 46° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个角的补角一定大于它本身 | |
| B. | 一个角的余角一定小于它本身 | |
| C. | 一个钝角减去一个锐角的差一定是一个锐角 | |
| D. | 一个角的余角一定小于其补角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在与国际友好学校交流活动中,小敏打算制做一个正方体礼盒送给外国朋友,每个面上分别书写一种中华传统美德,一共有“仁义礼智信孝”六个字.如图是她设计的礼盒平面展开图,那么“礼”字对面的字是( )
在与国际友好学校交流活动中,小敏打算制做一个正方体礼盒送给外国朋友,每个面上分别书写一种中华传统美德,一共有“仁义礼智信孝”六个字.如图是她设计的礼盒平面展开图,那么“礼”字对面的字是( )| A. | 义 | B. | 仁 | C. | 智 | D. | 信 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
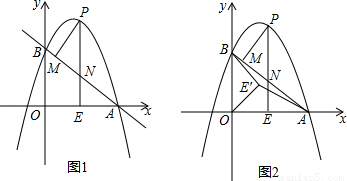
如图1,抛物线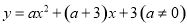 与
与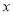 轴交于点A(4,0),与
轴交于点A(4,0),与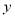 轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作
轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作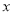 轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求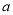 的值和直线AB的函数表达式;
的值和直线AB的函数表达式;
(2)在P点运动的过程中,请用含m的代数式表示线段PN;
(3)设△PMN的周长为 ,△AEN的周长为
,△AEN的周长为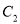 ,若
,若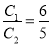 ,求m的值;
,求m的值;
(4)如图2,在(3)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接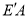 、
、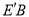 ,求
,求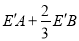 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com