
【题目】在平面直角坐标系![]() 中,
中,![]() 中的点
中的点![]() 是
是![]() 边上的一点,过点
边上的一点,过点![]() 的反比例函数
的反比例函数![]()
![]() 与
与![]() 边交于点
边交于点![]() ,连接
,连接![]() .
.
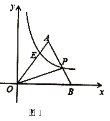
(1)如图1,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,求直线
的面积为5,求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
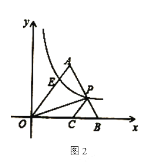
(2)如图2,若![]() ,过
,过![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,并且
,并且![]() 的面积为
的面积为![]() ,求反比例函数
,求反比例函数![]() 的解析式及点
的解析式及点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,见解析.
,见解析.
【解析】
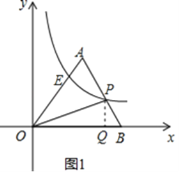
(1)过点P作PQ⊥x轴交x轴于点Q,利用待定系数法求出直线AB的解析式,根据△OPB的面积为5求出PQ的长,代入直线AB的解析式可得出P点坐标,进而可得出反比例函数的解析式;
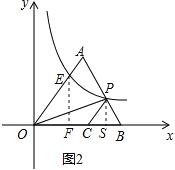
(2)过点E作EF⊥x轴交x轴于点F,过点P作PS⊥x轴交x轴于点S,利用锐角三角函数的定义求出OF及EF的长,故可得出反比例函数的解析式,根据△OPC的面积为![]() 求出OCPS的长,再由锐角三角函数的定义得出PS的长,进而可得出P点坐标.
求出OCPS的长,再由锐角三角函数的定义得出PS的长,进而可得出P点坐标.
解:(1)如图1,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 设直线
设直线![]() 的解析式为
的解析式为![]()
![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,
的面积为5,
![]()
![]() ,点
,点![]() 纵坐标为2.
纵坐标为2.
![]() 点
点![]() 在直线
在直线![]() 上
上![]() ,解得
,解得![]() .
.
![]() 点
点![]() 坐标为
坐标为![]()
![]() 此反比例函数的解析式为
此反比例函数的解析式为![]() ;
;
(2)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() ,
,
![]() 此反比例函数的解析式为
此反比例函数的解析式为![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 坐标为
坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】(原题)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB和∠COD都是直角,射线OE是∠AOC的平分线.
(1)把图中相等的角写出来,并说明它们相等的理由;
(2)若∠BOC=40°,直接写出∠BOD= 度,∠COE= 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的马路上有一个巡岗亭![]() ,巡岗员从岗亭
,巡岗员从岗亭![]() 出发以
出发以![]() 速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)第几次结束时巡逻员甲距离岗亭![]() 最远?距离
最远?距离![]() 有多远?
有多远?
(2)甲巡逻过程中配置无线对讲机,并一直与留守在岗亭![]() 的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°.
(1)尺规作图作出AB的垂直平分线DE,分别与AC、AB交于点D、E.并连结BD;(保留作图痕迹,不写作法)

(2)证明:△ABC∽△BDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com