
 �Ķ����ϣ�
�Ķ����ϣ����� ��1����P1M��l1��P2N��l2�����d��P1��l1����d��P2��l2�����ɵó��𰸣�
��2������P1M��l3��P2N��l3��ȷ��l3��P1P2��P1M+P2N��ֵ�����⼴�ɣ�
����P1M��l3��P2N��l3����P1����ԭ��ĶԳƵ�ΪP3����P3����l3�ľ���Ϊd3����l3��P3P2��P1M+P2N��ֵ�����⼴�ɣ�
��� �⣺��1����ͼ1����P1M��l1��P2N��l2��
��P1��4��0����l1��y=x��
��sin��1=$\frac{\sqrt{2}}{2}$��
��$\frac{M{P}_{1}}{4}$=$\frac{\sqrt{2}}{2}$
��MP1=2$\sqrt{2}$��
��P2��0��3����l2��y=$\sqrt{3}$x��
��sin��2=$\frac{1}{2}$��
��$\frac{{P}_{2}N}{3}$=$\frac{1}{2}$��
��$\frac{{P}_{2}N}{3}$=$\frac{3}{2}$��
d��P1��P2|l1��l2��=d��P1��l1��+d��l1��l2��+d��P2��l2��=2$\sqrt{2}$+0+$\frac{3}{2}$=$\frac{3}{2}$+2$\sqrt{2}$��
�ʴ�Ϊ��$\frac{3}{2}$+2$\sqrt{2}$��$\frac{3}{2}$+2$\sqrt{2}$��
��2������ͼ2����P1M��l3��P2N��l3��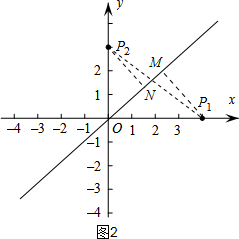
��P1M+P2N��P1P2��
�֡�d��P1��P2|l3��l3��=P1M+P2N��
�൱l3��P1P2��P1M+P2N��ֵ���
��k=tan��NOP1=$\frac{4}{3}$��
�ʴ�Ϊ��$\frac{4}{3}$��
����ͼ3����P1M��l3��P2N��l3����P1����ԭ��ĶԳƵ�ΪP3����P3����l3�ľ���Ϊd3��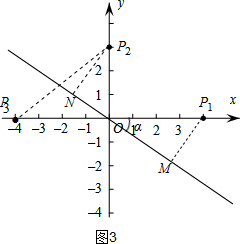
��d1=d3��
��d1+d3��P1P2��
�൱l3��P3P2��P1M+P2N��ֵ���
��k=tan��NOP3=-$\frac{4}{3}$��
���� ������Ҫ������һ�κ������ۺ��⣬����Ĺؼ�������d��P1��P2|l1��l2��=d��P1��l1��+d��l1��l2��+d��P2��l2�������壮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22•23=25 | B�� | ${��-2��^{-1}}=-\frac{1}{2}$ | C�� | ��25��5=225 | D�� | $\sqrt{��1-\sqrt{2}{��^2}}=1-\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A��˫����y=$\frac{k}{x}$�ϣ�AB��x����B��AC��y����C���ҡ�ABC�����Ϊ2����k=-4��
��ͼ����A��˫����y=$\frac{k}{x}$�ϣ�AB��x����B��AC��y����C���ҡ�ABC�����Ϊ2����k=-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
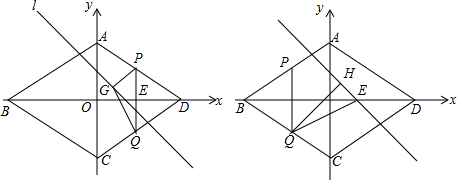
 ��ͼ���ڡ�ABC�У�2AB=3AC��ADΪ��BAC�Ľ�ƽ���ߣ���H���߶�AC�ϣ���CH=2AH��EΪBC�ӳ����ϵ�һ�㣬����EH���ӳ���AD�ڵ�G��ʹEG=ED������E��EF��AD�ڵ�F����AG��FG=4��7��
��ͼ���ڡ�ABC�У�2AB=3AC��ADΪ��BAC�Ľ�ƽ���ߣ���H���߶�AC�ϣ���CH=2AH��EΪBC�ӳ����ϵ�һ�㣬����EH���ӳ���AD�ڵ�G��ʹEG=ED������E��EF��AD�ڵ�F����AG��FG=4��7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
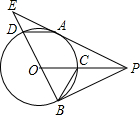 ��ͼ��PΪ��O��һ�㣬PA��PB�ֱ��С�O��A��B���㣬OP����O�ڵ�C������BO���ӳ�����O�ڵ�D����PA���ӳ����ڵ�E������AD��BC�����н��ۣ���AD��PO���ڡ�ADE�ס�PCB����tan��EAD=$\frac{ED}{EA}$����BD2=2AD•OP������һ����ȷ���ǣ�������
��ͼ��PΪ��O��һ�㣬PA��PB�ֱ��С�O��A��B���㣬OP����O�ڵ�C������BO���ӳ�����O�ڵ�D����PA���ӳ����ڵ�E������AD��BC�����н��ۣ���AD��PO���ڡ�ADE�ס�PCB����tan��EAD=$\frac{ED}{EA}$����BD2=2AD•OP������һ����ȷ���ǣ�������| A�� | �٢ۢ� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������������ת���ľ���ת��A��B�������ֳ���3�ȷݣ�
��ͼ��ʾ������������ת���ľ���ת��A��B�������ֳ���3�ȷݣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com