
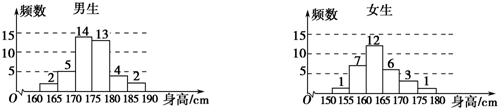
分析 (Ⅰ)由频率分步直方图知样本中男生人数为2+5+13+14+2+4,全校以10%的比例对全校700名学生按性别进行抽样检查,知道每个个体被抽到的概率是0.1,得到分层抽样比例为10%估计全校男生人数;
(Ⅱ)由题意知本题是一个古典概型,通过列举法看出试验发生包含的所有事件数,再从这些事件中找出满足条件的事件数,根据古典概型公式,得到结果
解答 解:(Ⅰ)样本中男生人数为2+5+13+14+2+4=40,
由分层抽样比例为10%估计全校男生人数为$\frac{40}{0.1}$=400;
(Ⅱ)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,
从上述6人中任取2人的树状图为:
∴从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185~190cm之间的可能结果数为9,
∴所求概率p2=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.同时考查了概率公式.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
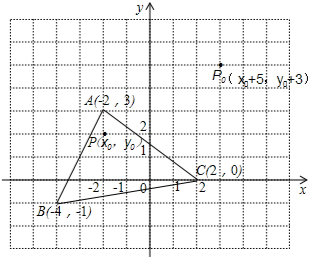 如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
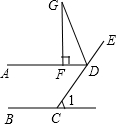 如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
如图,直线AD∥BC,点C、D、E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )| A. | 50° | B. | 30° | C. | 25° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.21a元 | B. | 1.1a元 | C. | 1.2a元 | D. | (0.2+a) 元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
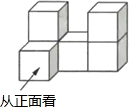 由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )
由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图、左视图和俯视图的面积,则( )| A. | 三个视图的面积一样大 | B. | 主视图的面积最小 | ||
| C. | 左视图的面积最小 | D. | 俯视图的面积最小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com