

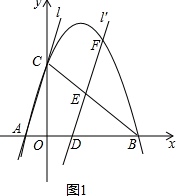
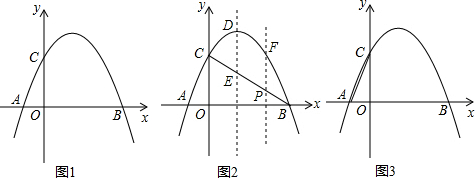
���� ��1��ͨ���ⷽ�̣�-$\frac{3}{8}$x2+$\frac{9}{4}$x+6=0�ɵ�A���B�����꣬�ټ����Ա���Ϊ0ʱ�ĺ���ֵ�ɵõ�C�����ꣻ
��2�����ݹ��ɶ������BC=10������֤��AB=BC������AC��FD���ó�$\frac{BE}{BC}$=$\frac{BD}{BA}$�����BE=BD������֤���ı���EB��DB�����Σ��ó�B��D��BC��Ȼ�����B����B��H��AB��H��֤�á�B��HD�ס�COB���������B��H=-$\frac{3}{5}$m+6��HD=-$\frac{4}{5}$m+8����һ�����OH���ó�B������ꣻ
��3���������ε����ʵó�BM=B��M����ƽ�ƵĶ����֪DE��AC������ƽ���߷��߶γɱ�������֤��BD=AD=$\frac{1}{2}$AB=5�����D�����꣬���ݹ��ɶ������AC�Ľ���ʽ���������DF�Ľ���ʽ��Ȼ���������̣��������F�����꣮
���  �⣺��1����y=0����y=-$\frac{3}{8}$x2+$\frac{9}{4}$x+6�ã�-$\frac{3}{8}$x2+$\frac{9}{4}$x+6=0��
�⣺��1����y=0����y=-$\frac{3}{8}$x2+$\frac{9}{4}$x+6�ã�-$\frac{3}{8}$x2+$\frac{9}{4}$x+6=0��
���x1=-2��x2=8��
���A��������-2��0������B��������8��0����
��x=0����y=-$\frac{3}{8}$x2+$\frac{9}{4}$x+6��y=6��
���C��������0��6����
��2����RT��COB�У��ɹ��ɶ�����BC=$\sqrt{B{O}^{2}+C{O}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10��
��AB=AO+OB=2+8=10��
��AB=BC��
��AD=m��
��DB=AB-AD=10-m��
��AC��FD��
��$\frac{BE}{BC}$=$\frac{BD}{BA}$��
��BE=BD=B��E=B��D=10-m��
���ı���EB��DB�����Σ�
��B��D��BC��
����B����B��H��AB��H��
���B��DH=��CBO����B��HD=��COB=90�㣬
���B��HD�ס�COB��
��$\frac{B��H}{CO}$=$\frac{HD}{OB}$=$\frac{B��D}{CB}$����$\frac{B��H}{6}$=$\frac{HD}{8}$=$\frac{10-m}{10}$��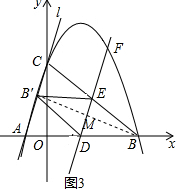
��B��H=-$\frac{3}{5}$m+6��HD=-$\frac{4}{5}$m+8��
����B����y����Ҳ�ʱ��OH=OB-HD-DB=8-��-$\frac{4}{5}$m+8��-��10-m��=$\frac{9}{5}$m-10��
����B����y������ʱ��OH=HD+DB-OB=��-$\frac{4}{5}$m+8��+��10-m��-8=10-$\frac{9}{5}$m��
���B���������$\frac{9}{5}$m-10��-$\frac{3}{5}$m+6����
��3�����ı���EB��DB�����Σ�
��BM=B��M��
��ƽ�ƵĶ����֪DE��AC��
��$\frac{BD}{AD}$=$\frac{BM}{B��M}$=1��
��BD=AD=$\frac{1}{2}$AB=5��
��OA=2��
��OD=3��
��D��������3��0����
��ֱ��AC�Ľ���ʽΪy=kx+b��
����A��-2��0����C��0��6���ã�$\left\{\begin{array}{l}{-2k+b=0}\\{b=6}\end{array}\right.$�����$\left\{\begin{array}{l}{k=3}\\{b=6}\end{array}\right.$��
��DF��AC��
��ֱ��DF�Ľ���ʽΪy=3x+b��
����D��3��0����9+b=0��
���b=-9��
��ֱ��DFΪy=3x-9��
��$\left\{\begin{array}{l}{y=3x-9}\\{y=-{\frac{3}{8}x}^{2}+\frac{9}{4}x+6}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1+\sqrt{41}}\\{y=3\sqrt{41}-12}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1-\sqrt{41}}\\{y=-12-3\sqrt{41}}\end{array}\right.$��
��F��������$\sqrt{41}$-1��3$\sqrt{41}$-12����
���� �����Ƕ��κ������ۺ��⣬�����˶��κ��������ʣ����ɶ�����Ӧ�ã���ԳƵ����ʣ�ƽ���߷��߶γɱ���������Ӧ�ã����������Ƶ��жϺ������Լ�����ϵ������һ�κ����Ľ���ʽ�ȣ�������������������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
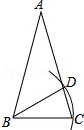 ��ͼ���ڡ�ABC�У�AB=AC����A=30�㣬��BΪԲ�ģ�BC�ij�Ϊ�뾶Բ������AC�ڵ�D������BD�����ABD=��������
��ͼ���ڡ�ABC�У�AB=AC����A=30�㣬��BΪԲ�ģ�BC�ij�Ϊ�뾶Բ������AC�ڵ�D������BD�����ABD=��������| A�� | 30�� | B�� | 60�� | C�� | 45�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�������ϣ�
�Ķ�������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
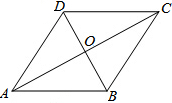 ��ͼ������ABCD�У���O�ǶԽ���AC��BD�Ľ��㣬��֪AB=5��OB=3��������ABCD�������24��
��ͼ������ABCD�У���O�ǶԽ���AC��BD�Ľ��㣬��֪AB=5��OB=3��������ABCD�������24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��ƽ�����£��棩 | 20 | 21 | 22 | 23 | 24 |
| ���� | 4 | 10 | 8 | 6 | 2 |
| A�� | 21��21 | B�� | 21��21.5 | C�� | 21��22 | D�� | 22��22 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ���뾶Ϊ30cm�����Ϊ450��cm2��������Ƥ������һ����Բ��������ģ�����Բ�ĵ���뾶rΪ��������
��ͼ����һ���뾶Ϊ30cm�����Ϊ450��cm2��������Ƥ������һ����Բ��������ģ�����Բ�ĵ���뾶rΪ��������| A�� | 5cm | B�� | 10cm | C�� | 15cm | D�� | 5��cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
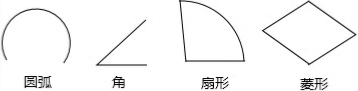
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com