
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①![]() 是
是![]() 的平分线;②
的平分线;②![]() ;③点
;③点![]() 在
在![]() 的垂直平分线上;④
的垂直平分线上;④![]()
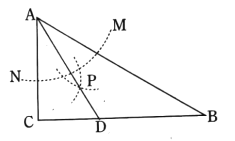
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
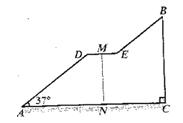
【题目】如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成.已知天桥高度BC≈4.8米,引桥水平跨度AC=8米.
(1)求水平平台DE的长度;
(2)若与地面垂直的平台立枉MN的高度为3米,求两段楼梯AD与BE的长度之比.
(参考:sin37°=0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区集体门票的收费标准是30人以内(含30人),每人25元;超过30人,超过部分每人10元.
(1)写出应收门票费![]() (元)与游览人数
(元)与游览人数![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)利用(1)中的函数关系式计算,某班54人去该风景区旅游时,为购门票共花了多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
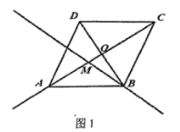
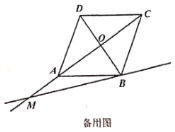
【题目】如图,![]() 为菱形
为菱形![]() 对角线的交点,
对角线的交点,![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() ,
,![]() ,
,![]() 都不重合),过点
都不重合),过点![]() ,
,![]() 分别向直线
分别向直线![]() 作垂线段,垂足分别为
作垂线段,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
(1)①当点![]() 在线段
在线段![]() 上时,在图1中依据题意补全图形:
上时,在图1中依据题意补全图形:
②猜想![]() 与
与![]() 的数量关系为 .
的数量关系为 .
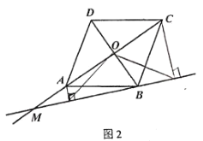
(2)小东通过观察、实验发现点![]() 在线段
在线段![]() 的延长线上运动时,(1)中的猜想始终成立.
的延长线上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明此猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与![]() 全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组![]() 和
和![]() ,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以
,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以![]() 和
和![]() 为对应边的全等三角形,即可证明猜想.
为对应边的全等三角形,即可证明猜想.
…
请你参考上面的想法,在图2中帮助小东完成画图,并证明此猜想(一种方法即可).
(3)当![]() 时,请直接写出线段
时,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系是 .
之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为![]() 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为![]() .
.
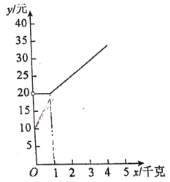
(1)写出![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(2)图中给出了![]() 与
与![]() 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若租用甲、乙两车各运12趟需支付运费4800元,且乙车每趟运费比甲车少200元.求单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF,交AC于点M,连结DE,BO.若∠BOC=60°,FO=FC,则下列结论:①AE=CF;②BF垂直平分线段OC;③△EOB≌△CMB;④四边形是BFDE菱形.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折和成综合成绩(综合成绩的满分仍为100分)
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(2)求出其余四名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com