

���� ��1���������߹���ƽ���ı��κ�ֱ�������Σ���֤��ƽ���ı��Σ�������ֱ��������б�����ߵ�OB��=OD�䣻
��2�������۵������ʵá�GHB��=��EB��H����GF��B��E���������۵��;��ε�ֱ�ǵá�GB��H=��B��D��E=90�㣬��GB���EF�����ı���GFEB��Ϊƽ���ı��Σ�
��3���������߹���ƽ�У�֤����ȵá�GB��O�ա�FNO��������ֱ��������б�����ߵ���б��һ��ɵý���
��� 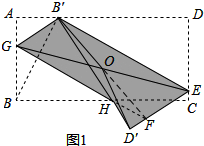 �⣺��1����ͼ1��OB��=OD�䣬�����ǣ�
�⣺��1����ͼ1��OB��=OD�䣬�����ǣ�
����OF��
���۵��ã���GB��H=��B=90�㣬��B��D��E=��D=90�㣬
���GB��H=��B��D��E��
��GB���EF��
ͬ����B��E��GF��
���ı���GFEB����ƽ���ı��Σ�
��OB��=OF��
��B�䡢O��F���ߣ�
��Rt��B��D��F�У�OD��=$\frac{1}{2}$B��F=OB�䣬
��OB��=OD�䣻
��2����ͼ1�����۵��ã���GHB=��GHB��=$\frac{1}{2}$��B��HB��
��DB��E=��D��B��E=$\frac{1}{2}$��D��B��D��
���ı���ABCDΪ���Σ�
��AD��BC��
���B��HB=��DB��D�䣬
���GHB��=��EB��H��
��GF��B��E��
�ߡ�GB��H=��B=90�㣬��B��D��E=��D=90�㣬
���GB��H=��B��D��E��
��GB���EF��
���ı���GB��EFΪƽ���ı��Σ�
��չ̽����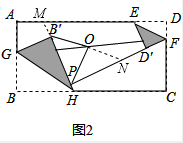
��ͼ2��OB��=OP�������ǣ�
�ӳ�HB�佻AD��M���ӳ�B��O��D��P�ڵ�N��
��B��HB=2��GHB����DED��=2��DEF����GHB=��DEF��
���B��HB=��DED�䣬
��AD��BC����DMH=��B��HB��
���DED��=��DMH��
��ED���MH��
���B��PN=��ED��F=90�㣬
���GB��P=��B��PN��
��GB���PD�䣬
���B��GO=��NFO��
�ߡ�GOB��=��FON��GO=OF��
���GB��O�ա�FNO��
��B��O=NO��
��B��O=OP��
���� �������ı��ε��ۺ��⣬�����˾��Ρ�ƽ���ı��κ�ֱ�������ε����ʣ�����������λ�ߵ����ʺ��ж���������������λ�ߵ����������У����������������������һ���ۣ�ͬʱ���Ҫע���۵������бߺͽǵĹ�ϵ��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-3 | B�� | x��-3��x��1 | C�� | x��1 | D�� | x��-3��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ķ�����ֵ��1+2+22+23+��+22016
���Ķ�����ֵ��1+2+22+23+��+22016�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com