解:(1)由观察可知:所得距离与这两个数的差的绝对值相等;
故答案为:所得距离与这两个数的差的绝对值相等;
(2)结合数轴,我们发现应分以下三种情况进行讨论.
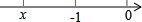
当x<-1时,距离为-x-1,
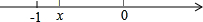
当-1<x<0时,距离为x+1,
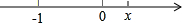
当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
若|x-6|=3,则x-6=±3,x=9或3;
故答案为:|x+1|;x=9或3;
(3)因为x为有理数,就是说x可以为正数,也可以为负数,也可以为0,所以要分情况讨论.
①当x<-1时,x-2<0,x+1<0,所以|x-1|+|x+3|=-(x-2)-(x+1)=-2x-1>3;
②当-1≤x<2时,x-2<0,x+1≥0,所以|x-1|+|x+3|=-(x-2)+(x+1)=3;
③当x≥2时,x-2≥0,x+1>0,所以|x-2|+|x+1|=(x-2)+(x+1)=2x-1≥3;
综上所述,当x=2或-1时,所以|x-2|+|x+1|的最小值是3.
故答案为:3;2或-1.
分析:(1)直接借助数轴可以得出;
(2)点B表示的数为-1,所以我们可以在数轴上找到点B所在的位置.那么点A呢?因为x可以表示任意有理数,所以点A可以位于数轴上的任意位置.那么,如何求出A与B两点间的距离呢?
结合数轴,我们发现应分以下三种情况进行讨论.
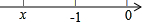
当x<-1时,距离为-x-1,
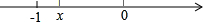
当-1<x<0时,距离为x+1,
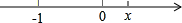
当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
若|x-6|=3,则x-6=±3,求出x即可;
(3)为x为有理数,所以要分类讨论x-1与x+3的正负,再去掉绝对值符号再计算.
点评:考查了数轴,借助数轴可以使有关绝对值的问题转化为数轴上有关距离的问题,反之,有关数轴上的距离问题也可以转化为绝对值问题.这种相互转化在解决某些问题时可以带来方便.事实上,|A-B|表示的几何意义就是在数轴上表示数A与数B的点之间的距离.

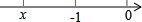
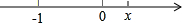
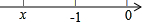
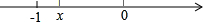
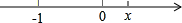


 学业测评一课一测系列答案
学业测评一课一测系列答案