练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，B、C分别在反比例函数与反比例函数的图象上，点A在x轴上，且四边形OABC是平行四边形，则四边形OABC的面积为         .

    3

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    11、如图，在锐角△ABC内有一点P，直线AP，BP，CP分别交对边于Q1，Q2，Q3，且∠PQ1C=∠PQ2A=∠PQ3B．
    试问：点P是否必为△ABC的垂心？如果是，请证明；如果不是，请举反例说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，已知P为正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．
    （1）试说明：BP=DP；
    （2）如图2，若正方形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？若是，请给予证明；若不是，请画图用反例加以说明；
    （3）试选取正方形ABCD的两个顶点，分别与正方形PECF的两个顶点连接，使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论；
    （4）旋转的过程中AP和DF的长度是否相等，若不等，直接写出AP：DF=
     
    ；
    （5）若正方形ABCD的边长是4，正方形PECF的边长是1．把正方形PECF绕点C按逆时针方向旋转的过程中，△PBD的面积是否存在最大值、最小值？如果存在，试求出最大值、最小值；如果不存在，请说明理由．
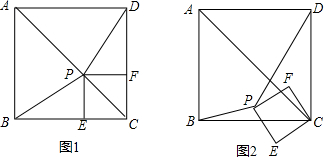
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，已知P为正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．
    （1）试说明：BP=DP；
    （2）如图2，若正方形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？若是，请给予证明；若不是，请画图用反例加以说明；
    （3）试选取正方形ABCD的两个顶点，分别与正方形PECF的两个顶点连接，使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论；
    （4）旋转的过程中AP和DF的长度是否相等？若不等，直接写出AP：DF=
     
    ；
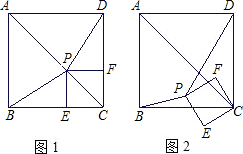    （5）若正方形ABCD的边长是4，正方形PECF的边长是1．把正方形PECF绕点C按逆时针方向旋转精英家教网的过程中，△PBD的面积是否存在最大值、最小值？如果存在，试求出最大值、最小值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

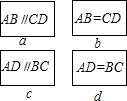    小亮同学为了巩固自己对平行四边形判定知识的掌握情况，设计了一个游戏，他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上，卡片如图：
    他将卡片正面朝下反扣在桌面上，洗匀后从中随机抽取两张，然后根据卡片上的两个条件判断四边形ABCD是否为平行四边形，请你用列举法（列表法或树状图法）求出他能够判定四边形ABCD为平行四边形的概率．（卡片可用a、b、c、d表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图14所示，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数y=ax2+[x/6]+c的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）。已知AM=BC。

    [1]求二次函数的解析式；

    [2]证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；

    [3]在[2]的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N。

    ①若直线l⊥BD，如图14所示，试求[1/BP]+[1/BQ]的值；

    ②若l为满足条件的任意直线。如图15所示，①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例。

     


    查看答案和解析>>

    同步练习册答案