
【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
【答案】(1)|x+2|;(2)表示的是x与(-6)之间的距离,x=-2;(3)P点表示的数为-4;(4)![]() ,
,![]() 或
或![]() ,
,![]() (5)B点向左移动
(5)B点向左移动![]() 此时P点向右移动
此时P点向右移动![]() 或B点向右移动
或B点向右移动![]() 此时P点向左移动
此时P点向左移动![]() .
.
【解析】
(1)根据题中的公式,代入即可;
(2)第一个空,|x+6|=|x- (-6)|,根据距离公式填写即可,第二个空两个数的绝对值相等,这两个数相等或这两个数互为相反数,据此列出两个方程求解即可;
(3)画出数轴,据图可得答案;
(4)根据题意M、N距离-3的距离都为![]() ,设距离-3的距离为
,设距离-3的距离为![]() 的数为x,据此列出含绝对值的方程,解方程即可;
的数为x,据此列出含绝对值的方程,解方程即可;
(5)设B点为x,表示出P点,分①BP=AP②BP=AB③AP=AB三种情况讨论即可.
(1)|x-(-2)|=|x+2|,故表示为|x+2|;
(2)∵|x+6|=|x-(-6)|,
∴表示的是x与(-6)之间的距离,
∵|x+6|= |x -2|
∴x+6=x-2或x+6=-(x-2)
解x+6=x-2无解,解x+6=-(x-2)得x=-2.
则x=-2.
(3)如下图,易得对称轴为经过-3且与数轴垂直的直线,所以P点表示的数为-4.

(4)根据题意M、N在-3的左右两边,且距离-3的距离为![]() ,设距-3的距离为
,设距-3的距离为![]() 的数为x,则|x+3|=
的数为x,则|x+3|=![]() ,即x+3=
,即x+3=![]() ,x=
,x=![]() 或x=
或x=![]() ,故M点为
,故M点为![]() 时N为
时N为![]() ,M点为
,M点为![]() 时N为
时N为![]() .
.
(5)设B点移动后表示的数为x,P点表示的数为y,则有|x-3|=|y-3|, x-3=y-3或x-3=3-y,解x-3=y-3得x=y,即B、P两点重合舍去,解x-3=3-y得y= -x-6,所以P点表示的数位-x-6所以AB=|1-x|,AP=|1-(-x-6)|=|7+x|,BP=|x-(-x-6)|=|2x+6|.
根据移动后相邻两点间距离相等,可分三类情况
①BP=AP,即|2x+6|=|7+x|即2x+6=7+x或2x+6=-7-x,
解2x+6=7+x得x=1,即A、B两点重合不符合题意舍去,
解2x+6=-7-x得![]() ,所以B点向左移动
,所以B点向左移动![]() 即可,此时P点向右移动
即可,此时P点向右移动![]() ;
;
②BP=AB,即|2x+6|=|1-x|即2x+6=1-x,或2x+6=x-1,
解2x+6=1-x得x=![]() ,所以B点向右移动
,所以B点向右移动![]() ,此时P点向左移动
,此时P点向左移动![]() ,
,
解2x+6=x-1得x=-7,此时-x-6=1,A、P两点重合舍去;
③AP=AB,则|1-x|=|7+x|,即1-x=7+x或x-1=7+x
解1-x=7+x得x=3,此时B、P重合舍去,
解x-1=7+x无解舍去.
故B点向左移动![]() 此时P点向右移动
此时P点向右移动![]() 或B点向右移动
或B点向右移动![]() 此时P点向左移动
此时P点向左移动![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中: ①abc<0;②4ac﹣b2>0;③a﹣b+c>2;④a<b<0;⑤ac+2=b,
正确的个数有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
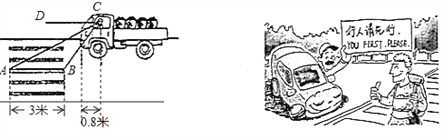
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价![]() 元,
元,
(1)降价![]() 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含![]() 的代数式表示);
的代数式表示);
(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,线段AC=10 cm,BC=4 cm,取线段AC、BC的中点D、E.
![]()
(1)请你计算线段DE的长是多少?
(2)观察DE的大小与线段AB的关系,你能用一句简洁的话将这种关系表述出来吗?
(3)若点C为直线AB上的一点,其他条件不变,线段DE的长会改变吗?如果改变,请你求出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一次函数y1=-x-2与y2=x-4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=-x-2与y2=x-4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与y轴交于点
与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,点B坐标为
,点B坐标为![]() .
.
![]() 求二次函数解析式及顶点坐标;
求二次函数解析式及顶点坐标;
![]() 过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点
过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点![]() 点P在AC上方
点P在AC上方![]() ,作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
,作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com