
 如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.
如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1. 分析 由三角形的面积入手,即S△PBC+S△PAC+S△PAB=S△ABC,通过化简可得面积与线段之间的关系,进而即可求解.
解答 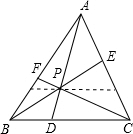 解:∵S△PBC+S△PAC+S△PAB=S△ABC①
解:∵S△PBC+S△PAC+S△PAB=S△ABC①
∴$\frac{{S}_{△PBC}}{{S}_{△ABC}}$+$\frac{{S}_{△PAC}}{{S}_{△ABC}}$+$\frac{{S}_{△PAB}}{{S}_{△ABC}}$=1,②
由面积概念得:$\frac{{S}_{△PDC}}{{S}_{△ADC}}$=$\frac{PD}{AD}$,$\frac{{S}_{△PDB}}{{S}_{△ADB}}$=$\frac{PD}{AD}$,
∴$\frac{{S}_{△PDC}{+S}_{△PDB}}{{S}_{△ADC}{+S}_{△ADB}}$=$\frac{PD}{AD}$,
即$\frac{{S}_{△PBC}}{{S}_{△ABC}}$=$\frac{PD}{AD}$③
同理得:$\frac{{S}_{△PAC}}{{S}_{△ABC}}$=$\frac{PE}{BE}$④
$\frac{{P}_{△PAB}}{{S}_{△ABC}}$=$\frac{PF}{CF}$⑤
把式③、④、⑤、代入式②得:$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.
故答案为:1.
点评 本题主要考查了三角形的面积比与对应边的比值之间的关系,能够熟练掌握其内在联系,并能求解一些比较复杂的问题.


科目:初中数学 来源: 题型:解答题
 大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:
大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
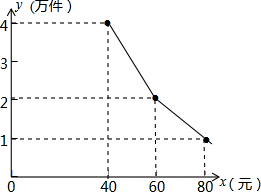 为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.
为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 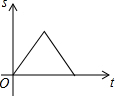 | B. |  | C. |  | D. | 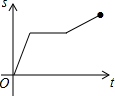 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com