
 工厂有一批长3dm、宽2dm的矩形铁片,为了利用这批材料,在每一块上裁下一个最大的圆铁片⊙O1之后(如图所示),再在剩余铁片上裁下一个充分大的圆铁片⊙O2.
工厂有一批长3dm、宽2dm的矩形铁片,为了利用这批材料,在每一块上裁下一个最大的圆铁片⊙O1之后(如图所示),再在剩余铁片上裁下一个充分大的圆铁片⊙O2.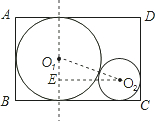 解:(1)如图,矩形ABCD中,AB=2r1=2dm,即r1=1dm.…(1分)
解:(1)如图,矩形ABCD中,AB=2r1=2dm,即r1=1dm.…(1分)| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
工厂有一批长3dm、宽2dm的矩形铁片,为了利用这批材料,在每一块上裁下一个最大的圆铁片⊙O1之后(如图所示),再在剩余铁片上裁下一个充分大的圆铁片⊙O2.
1.(1)求⊙O1、⊙O2的半径r1、r2的长;
2.(2)能否在剩余的铁片上再裁出一个与⊙O2同样大小的圆铁片?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届北京市燕山区九年级上学期期末考试数学卷 题型:解答题
工厂有一批长3dm、宽2dm的矩形铁片,为了利用这批材料,在每一块上裁下一个最大的圆铁片⊙O1之后(如图所示),再在剩余铁片上裁下一个充分大的圆铁片⊙O2.
【小题1】(1)求⊙O1、⊙O2的半径r1、r2的长;
【小题2】(2)能否在剩余的铁片上再裁出一个与⊙O2同样大小的圆铁片?为什么?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市燕山区九年级上学期期末考试数学卷 题型:解答题
工厂有一批长3dm、宽2dm的矩形铁片,为了利用这批材料,在每一块上裁下一个最大的圆铁片⊙O1之后(如图所示),再在剩余铁片上裁下一个充分大的圆铁片⊙O2.
1.(1)求⊙O1、⊙O2的半径r1、r2的长;
2.(2)能否在剩余的铁片上再裁出一个与⊙O2 同样大小的圆铁片?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com