
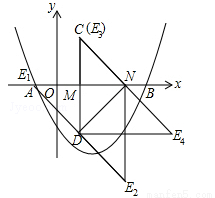
����������12�֣���ͼ�����κ���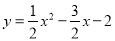 ��ͼ����x�ύ�ڵ�A��B����M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN��2����MNΪֱ�DZ�����������ֱ��������CMN����CMN��90�㣮���M�ĺ�����Ϊm��
��ͼ����x�ύ�ڵ�A��B����M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN��2����MNΪֱ�DZ�����������ֱ��������CMN����CMN��90�㣮���M�ĺ�����Ϊm��
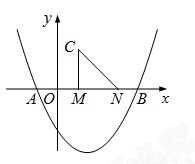
��1������C��������������ʱ����m��ֵ��
��2�����߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN��
�ٵ���D�����������ߵĶԳ�����ʱ�����D�����꣮
����DNΪֱ�DZ�������ֱ��������DNE������E�����������ߵĶԳ�����ʱ����m��ֵ��
��1��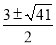 ����2���٣�
����2���٣�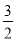 ����2������
����2������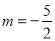 ��
��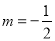 ��
��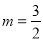 ��
��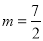 ��
��
��������
�����������1���ȸ��ݵ���ֱ�������ε����������C������Ϊ��m��2�����ٽ�C��������� ���������m��ֵ��
���������m��ֵ��
��2����������ת�����ʵó���D������Ϊ��m����2�����ٸ��ݶ��κ������������������ �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ�� ��Ȼ����ݵ�D��ֱ��
��Ȼ����ݵ�D��ֱ�� �ϣ����������D�����ꣻ
�ϣ����������D�����ꣻ
����DNΪֱ�DZ�������ֱ��������DNEʱ���ֱ���D��NΪֱ�Ƕ��㣬��DN������ֱ���������ֱ��������DNE��E���λ�÷�����������ۣ����ÿһ��������������ȸ��ݵ���ֱ�������ε����������E�����꣬Ȼ����ݵ�E��ֱ�� �ϣ��г�����m�ķ��̣��ⷽ�̼������m��ֵ��
�ϣ��г�����m�ķ��̣��ⷽ�̼������m��ֵ��
�����������1���ߡ�CMN�ǵ���ֱ��������CMN����CMN=90�㣬��CM=MN=2�����C������Ϊ��m��2�����ߵ�C��m��2�����������ϣ���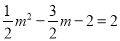 �����
�����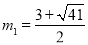 ��
��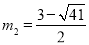 �����C��������������ʱ��m��ֵΪ
�����C��������������ʱ��m��ֵΪ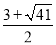 ��
��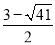 ��
��
��2���١߽��߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN�����CND=90�㣬DN=CN=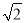 CM=
CM=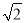 MN����CD=
MN����CD=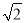 CN=2CM=2MN����DM=CM=MN����DMN=90�㣬���D������Ϊ��m����2�����֡�������
CN=2CM=2MN����DM=CM=MN����DMN=90�㣬���D������Ϊ��m����2�����֡������� �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ�� ����D�����������ߵĶԳ����ϣ����D������Ϊ��
����D�����������ߵĶԳ����ϣ����D������Ϊ��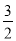 ����2����
����2����
����ͼ����DNΪֱ�DZ�������ֱ��������DNE��E���λ����������������E����E1��λ��ʱ���ߵ�D������Ϊ��m����2����MN=ME1=2����N������Ϊ��m+2��0�������E1�ģ�m��2��0�����ߵ�E1�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���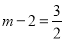 �����
�����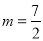 ��
��
���E����E2��λ��ʱ���ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E2�ģ�m+2����4�����ߵ�E2�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���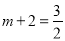 �����
����� ��
��
���E����E3��λ��ʱ���ߵ�D������Ϊ��m����2�������E3�ģ�m��2�����ߵ�E3�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���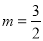 ��
��
���E����E4��λ��ʱ���ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E4�ģ�m+4����2�����ߵ�E4�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���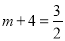 �����
�����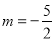 ��
��
���Ͽ�֪������E�����������ߵĶԳ�����ʱ�����з���������m��ֵΪ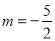 ��
��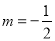 ��
��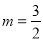 ��
��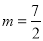 ��
��
���㣺���κ����ۺ��⣮


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�ڵڶ������������ѧ�Ծ��������棩 ���ͣ������
������y=��x2�Ķ�������Ϊ________������A��3��m���Ǵ���������һ�㣬��m= ____���Ѵ�����������ƽ��4����λ�õ��������ߵĺ�����ϵʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶11�½��Լ����ѧ�Ծ��������棩 ���ͣ�ѡ����
���к����ж��κ����ǣ� ��
A��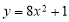 B��
B��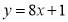 C��
C��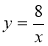 D��
D��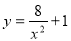
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б�Ӧ�ؾ��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
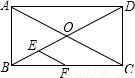
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB=60�㣬��E��F�ֱ���BO��BC���е㣬��AB=6cm�����BEF���ܳ�Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б�Ӧ�ؾ��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����֪ABΪ��O��ֱ������C��D�ڡ�O�ϣ���ABC=50�㣬���D�Ķ���Ϊ�� ��

A��30�� B��40�� C��50�� D��60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�γ����ζ������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
����������10�֣��γǹ������г���Ŀ����ȫ�����ɣ��γ�����250��վ�㣬�ۼ�Ͷ��6000�����г���Ϊ���ǵ���������˷��㣮ͼ��1����ʾ�������г���ʵ��ͼ��ͼ��2����һ�����г��IJ��ּ���ʾ��ͼ�����г��ܵ�AC�ij�Ϊ45cm���ҡ�CAB��75�㣬��CBA=50�㣮���ο����ݣ�sin75���0.96��cos75���0.26��tan75���3.73 ��sin50���0.76��cos50���0.64��tan50���1.19��

��1�������̶���C�����ܵ�AB�ľ��룻
��2���ܵ�AB�ij��������ȷ��1cm����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�γ����ζ������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ͼ����һ��ĸ�߽�Բ���������չƽ���õ�һ�����Σ���Բ�ĵ���Բ�İ뾶r��2cm�����ε�Բ�ĽǦȣ�120�㣬���Բ��ĸ�߳�lΪ cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪AB�ǡ�O��ֱ����AB��8����C�ڰ뾶OA�ϣ���C���O��A���غϣ�������C��AB�Ĵ��߽���O�ڵ�D������OD������B��OD��ƽ���߽���O�ڵ�E��������CD�ڵ�F��
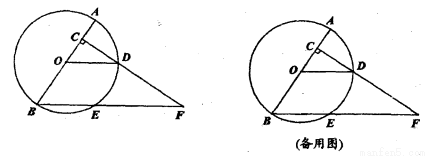
��1����ED��BE�����F�Ķ�����
��2�����߶�OC��a�����߶�BE��EF�ij����ú�a�Ĵ���ʽ��ʾ����
��3�����C����ֱ��OD�ĶԳƵ�ΪP������PBEΪ���������Σ���OC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�����ʡ�����о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
 ��ƽ������
��ƽ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com