
分析 先找出1+$\sqrt{1+x}$和1-$\sqrt{1-x}$有理化因式,再根据二次根式的性质进行化简后代入求值即可.
解答 解:$\frac{1+x}{1+\sqrt{1+x}}$+$\frac{1-x}{1-\sqrt{1-x}}$
=$\frac{(1+x)(1-\sqrt{1+x})}{(1+\sqrt{1+x})(1-\sqrt{1+x})}$+$\frac{(1-x)(1+\sqrt{1-x})}{(1-\sqrt{1-x})(1+\sqrt{1-x})}$
=$\frac{(1+x)(1-\sqrt{1+x})}{-x}+\frac{(1-x)(1+\sqrt{1-x})}{x}$
=$\frac{\sqrt{1+x}+x\sqrt{1+x}-1-x+1+\sqrt{1-x}-x-x\sqrt{1-x}}{x}$
=$\frac{\sqrt{1+x}+\sqrt{1-x}}{x}+\sqrt{1+x}-\sqrt{1-x}-2$,
∵$(\frac{\sqrt{3}+1}{2})^{2}$=$\frac{2+\sqrt{3}}{2}$,
∴$\sqrt{\frac{2+\sqrt{3}}{2}}$=$\frac{\sqrt{3}+1}{2}$,
∵$(\frac{1-\sqrt{3}}{2})^{2}$=$\frac{2-\sqrt{3}}{2}$,
∴$\sqrt{\frac{2-\sqrt{3}}{2}}$=$\frac{1-\sqrt{3}}{2}$,
把x=$\frac{\sqrt{3}}{2}$代入代数式可得:
原式=$\frac{\sqrt{1+\frac{\sqrt{3}}{2}}+\sqrt{1-\frac{\sqrt{3}}{2}}}{\frac{\sqrt{3}}{2}}$+$\sqrt{1+\frac{\sqrt{3}}{2}}$-$\sqrt{1-\frac{\sqrt{3}}{2}}$-2
=$\frac{\sqrt{\frac{2+\sqrt{3}}{2}}+\sqrt{\frac{2-\sqrt{3}}{2}}}{\frac{\sqrt{3}}{2}}$+$\sqrt{\frac{2+\sqrt{3}}{2}}$-$\sqrt{\frac{2-\sqrt{3}}{2}}$-2
=$\frac{\frac{\sqrt{3}+1}{2}+\frac{1-\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$+$\frac{\sqrt{3}+1}{2}$-$\frac{1-\sqrt{3}}{2}$-2
=$\frac{2}{\sqrt{3}}$+$\sqrt{3}$-2
=$\frac{2\sqrt{3}}{3}$+$\sqrt{3}$-2
=$\frac{5\sqrt{3}}{3}$-2.
点评 本题考查了二次根式的化简求值,解题的关键是化简二次根式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.
如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
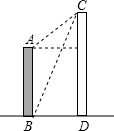 小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )| A. | 2a+2b | B. | 2b+3 | C. | 2a-3 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.
由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com