Question

6．如图（1），在矩形ABCD中，AB=6，BC=2$\sqrt{3}$，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，如图（2）以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t＞0）．
（1）如图（3），当等边△EFG的边FG恰好经过点C时，求运动时间t的值；
（2）如图（4），当等边△EFG的顶点G恰好落在CD边上时，求运动时间t的值；
（3）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请求出S与t之间的函数关系式，并写出相应的自变量，的取值范围．

Answer 1

分析 （1）当边FG恰好经过点C时，∠CFB=60°，BF=3-t，在Rt△CBF中，解直角三角形可求t的值；
（2）利用当等边△EFG的顶点G恰好落在CD边上时，OG垂直平分EF，进而得出t的值；
（3）按照等边△EFG和矩形ABCD重叠部分的图形特点，分为0≤t＜1，1≤t＜3，3≤t＜4，4≤t＜6四种情况，分别写出函数关系式．

解答 解：（1）当边FG恰好经过点C时，（如图1）
∠CFB=60°，BF=3-t，
在Rt△CBF中，BC=2$\sqrt{3}$，
tan∠CFB=$\frac{BC}{BF}$，
∴tan60°=$\frac{2\sqrt{3}}{BF}$，
∴BF=2，
即3-t=2，
∴t=1，
∴当边FG恰好经过点C时，t=1．   
          
（2）当点G在CD边上时，如图2，
此时FB=t-3，AE=t-3，
得OE=OF．
∴OG垂直平分EF
∵OG=AD=2$\sqrt{3}$，
∴OE=$\frac{OG}{tan60°}$=2，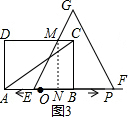
∴AE=t-3=1，
解得：t=4；
                          
（3）依题意可知，当t=3时，F点到B点，E点到A点；当t=6时，E、F两点相遇，停止运动．分四种情形讨论：
①当0＜t≤1时，如图3所示．
此时重叠部分面积S=S梯形_BCME=$\frac{1}{2}$（MC+BE）=BC，
∵MN=2$\sqrt{3}$，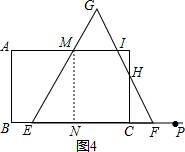
∴EN=2，
而BE=OB+OE=3+t，
∴BN=CM=3+t-2=1+t
S=$\frac{1}{2}$（1+t+3+t）×2$\sqrt{3}$=2$\sqrt{3}$t+4$\sqrt{3}$，
②当1≤t≤3时，如图4所示：
此时重叠部分的面积S=S_{五边形ECHIM}=S_△GEF-S_△HCF-S_△GMI
此时PF=t，BE=3-t，所以EF=6，△GEF是边长为6的正三角形
∵MN=2$\sqrt{3}$，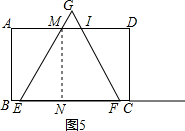
∴ME=4，得GM=2，三角形GMI是边长为2的正三角形
∵CF=3-t，∴HC=$\sqrt{3}$（3-t），
∴S=$\frac{1}{2}×6×3\sqrt{3}$-$\frac{1}{2}$×2×$\sqrt{3}$-$\frac{1}{2}$×（3-t）²×$\sqrt{3}$=-$\frac{\sqrt{3}}{2}$（t-3）²+8$\sqrt{3}$；
③当3＜t≤4时，如图5所示
此时重叠部分的面积S=S_梯形EFIM=$\frac{1}{2}$（EF+MI）MN，
此时，CF=BE=t-3，EF=12-2t，
∵MN=2$\sqrt{3}$，∴ME=4，∴MG=12-2t-4=8-2t，三角形GMI是边长为8-2t的正三角形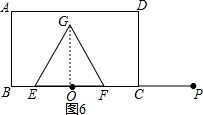
∴S=$\frac{1}{2}$（12-2T+8-2T）×$2\sqrt{3}$=-4$\sqrt{3}$t+20$\sqrt{3}$；
④当4＜t≤6时，如图6所示：
此时，CF=BE=t-3，EF=12-2t，O为EF的中点，GO⊥EF
此时重叠部分的面积S=S_△GEF=$\frac{1}{2}$EF•GO，
∵EF=12-2t，∴EO=6-t，GO=$\sqrt{3}$EO=$\sqrt{3}$（6-t），
∴S=$\frac{1}{2}$（12-2t）×$\sqrt{3}$（6-t）=$\sqrt{3}$（t-6）²，
综上所述：S=$\left\{\begin{array}{l}{2\sqrt{3}t+4\sqrt{3}（0＜t≤1）}\\{-\frac{\sqrt{3}}{2}（t-3）^{2}+8\sqrt{3}（1＜t≤3）}\\{-4\sqrt{3}t+20\sqrt{3}（3＜t≤4）}\\{\sqrt{3}（t-6）^{2}（4＜t≤6）}\end{array}\right.$．

点评 本题考查了等边三角形的性质、矩形的性质、解直角三角形的有关知识以及多边形面积求法，关键是根据特殊三角形的性质，分类讨论得出．