


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线![]() 上,
上,
1.点A的坐标为__________,点B的坐标为___________;抛物线的解析式为_________;
2.在抛物线上是否还存在点P(点B除外),使△ACP是以AC为直角边向直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由
3.若点D是(1)中所求抛物线在第三象限内的一个动点,连结BD、CD。当△BCD的面积最大时,求点D的坐标。
4.若点P是(1)中所求抛物线上一个动点,以线段AB、BP为邻边作平形四边形ABPQ。当点Q落在x轴上时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
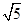 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线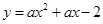 上,
上,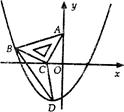
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南安阳九年级5月中考模拟考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,将一块腰长为 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线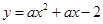 上,
上,
1.点A的坐标为__________,点B的坐标为___________;抛物线的解析式为_________;
2.在抛物线上是否还存在点P(点B除外),使△ACP是以AC为直角边向直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由
3.若点D是(1)中所求抛物线在第三象限内的一个动点,连结BD、CD。当△BCD的面积最大时,求点D的坐标。

4.若点P是(1)中所求抛物线上一个动点,以线段AB、BP为邻边作平形四边形ABPQ。当点Q落在x轴上时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com