
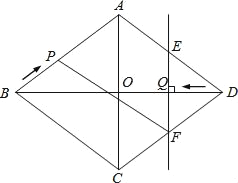
【题目】如图,在菱形ABCD中,AC,BD交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为lcm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为lcm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q.F,当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)求菱形ABCD的面积;
(2)当t=1时,求QF长;
(3)是否存在某一时刻t,使四边形APFD是平行四边形?若存在,求出t值,若不存在,请说明理由;
(4)设△DEF的面积为s(cm2),试用含t的代数式表示S,并求t为何值时,△DEF的面积与△BPC的面积相等.
【答案】(1)96(cm2);(2)![]() ;(3)当t=
;(3)当t=![]() s时,四边形APFD是平行四边形.(4)S=
s时,四边形APFD是平行四边形.(4)S=![]() t2,当t=
t2,当t=![]() 时,△DEF的面积与△BPC的面积相等
时,△DEF的面积与△BPC的面积相等
【解析】
菱形面积=![]() ×AC×BD;
×AC×BD;
由EF∥AC,可得![]() ,即可求QF的长;
,即可求QF的长;
(3)当AP=DF时,四边形APFD为平行四边形,用t表示出AP=10-t,DF=
![]() t,列等式计算;
t,列等式计算;
(4)用t表示出△DEF和△BPC的面积,令其相等,即可求.
解:(1)∵四边形ABCD是菱形,AC=12cm,BD=16cm,
∴菱形ABCD的面积为![]() ×12×16=96(cm2).
×12×16=96(cm2).
(2)∵AB∥CD,AC⊥BD,OA=OC=6cm,OB=OD=8cm,
在![]() 中,AB=
中,AB=![]() (cm),
(cm),
当t=1时,DQ=1,
∵EF⊥BD,AC⊥BD,
∴EF∥AC,
∴![]() ,
,
∴![]() ,
,
∴QF=![]() (cm).
(cm).
(3)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=6,OB=OD=8.
在![]() 中,AB=
中,AB=![]() .
.
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴![]() ,
,
即![]() ,
,
∴DF=![]() t.
t.
∵四边形APFD是平行四边形,
∴AP=DF.
即10﹣t=![]() t,
t,
解这个方程,得t=![]() .
.
∴当t=![]() s时,四边形APFD是平行四边形.
s时,四边形APFD是平行四边形.
(4)S=S△DEF=![]() .
.
如图作CG⊥AB于点G.
∵S菱形ABCD=ABCG=![]() ACBD,
ACBD,
即10CG=![]() ×12×16,
×12×16,
∴CG=![]() ,
,
∴S△BPC=![]() t×
t×![]() =
=![]() t,
t,
当△DEF的面积与△BPC的面积相等时,
![]() ,
,
解得t=![]() 或t=0(舍弃),
或t=0(舍弃),
∴S=![]() ,当t=
,当t=![]() 时,△DEF的面积与△BPC的面积相等
时,△DEF的面积与△BPC的面积相等


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AE⊥BC于E,将△ABE沿AE所在直线翻折得△AEF,若AB=2,∠B=45°,则△AEF与菱形ABCD重叠部分(阴影部分)的面积为( ).
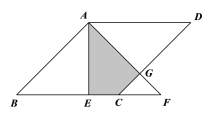
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,分别以
,分别以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() .
.
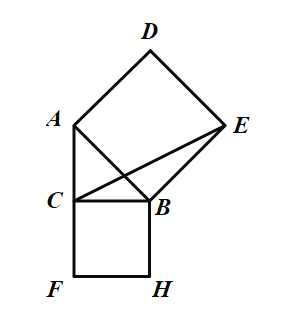

(1)当![]() 时,正方形
时,正方形![]() 的周长
的周长![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(2)连接![]() .试说明:三角形
.试说明:三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的一半.
面积的一半.
(3)已知![]() ,且点
,且点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是线段
是线段![]() 上的动点,当
上的动点,当![]() 点和
点和![]() 点在移动过程中,
点在移动过程中,![]() 的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
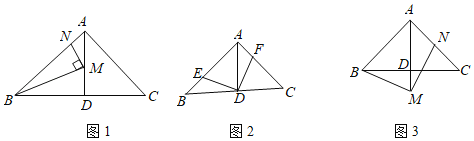
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .
.
(1)如图1,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,当
,当![]() ,
,![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)如图2,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数;
(3)在△ABC中,AB=4,AC=2,AD是△ABC的优美线,且△ABD是等腰三角形,直接写出优美线AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
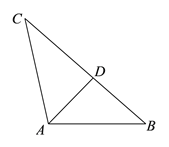
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点![]() 出发,在矩形
出发,在矩形![]() 边上沿着
边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知机器人的速度为1个单位长度
时停止移动.已知机器人的速度为1个单位长度![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要![]() (即在
(即在![]() 、
、![]() 处拐弯时分别用时
处拐弯时分别用时![]() ).设机器人所用时间为
).设机器人所用时间为![]() 时,其所在位置用点
时,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图象如图②所示.
的函数图象如图②所示.
(1)求![]() 、
、![]() 的长;
的长;
(2)如图②,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,线段
上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,设机器人用了
,设机器人用了![]() 到达点
到达点![]() 处,用了
处,用了![]() 到达点
到达点![]() 处(如图①).若
处(如图①).若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
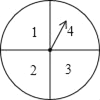
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com