
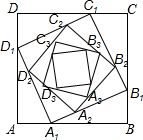
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
分析 首先由勾股定理求得A1B12与A2B22,即可求得正方形A1B1C1D1与正方形A2B2C2D2的面积,然后得规律:正方形AnBnCnDn的面积=($\frac{5}{9}$)na2.
解答 解:在Rt△A1BB1中,由勾股定理可知;A1B12=A1B2+B1B2=($\frac{2}{3}$a)2+($\frac{1}{3}$a)2=$\frac{5}{9}$a2,即正方形A1B1C1D1的面积=$\frac{5}{9}$a2;
在Rt△A2B1B2中,由勾股定理可知:A2B22=A2B12+B2B12=($\frac{2}{3}$×$\frac{\sqrt{5}}{3}$a)2+($\frac{1}{3}$×$\frac{\sqrt{5}}{3}$a)2=($\frac{5}{9}$)2a2;即正方形A2B2C2D2的面积=($\frac{5}{9}$)2a2;
…
∴正方形AnBnCnDn的面积=($\frac{5}{9}$)na2.
故选D.
点评 此题考查了正方形的性质以及勾股定理.属于规律性题目,得到规律正方形AnBnCnDn的面积=($\frac{5}{9}$)na2是关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )
如图,从一艘船上测得一个灯塔的方向是北偏西47°,那么这艘船在这个灯塔的( )| A. | 南偏东47° | B. | 南偏东43° | C. | 南偏西47° | D. | 南偏西43° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 238×103 | B. | 2.38×105 | C. | 23.8×104 | D. | 0.238×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
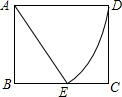 如图,矩形ABCD中,AD=4,AB=2$\sqrt{3}$,以点A为圆心,AD为半径画弧交BC于点E,所得的扇形的弧长为$\frac{4π}{3}$.
如图,矩形ABCD中,AD=4,AB=2$\sqrt{3}$,以点A为圆心,AD为半径画弧交BC于点E,所得的扇形的弧长为$\frac{4π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com