
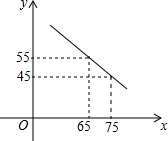
 某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.
某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.分析 (1)将一次函数的图象经过的两点的坐标代入到直线的解析式即可确定其表达式;
(2)根据题意列出二次函数表达式,配方成顶点式,运用二次函数的性质解决实际问题即可;
(3)利用单件的利润×销量=总利润即可列出方程求解.
解答 解:(1)设一次函数关系式为y=kx+b
由图象可知:直线过(65,55),(75,45)两点
所以有:$\left\{\begin{array}{l}{65k+b=55}\\{75k+b=45}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=120}\end{array}\right.$
∴y与x的函数关系式为:y=-x+120;
(2)依题意得:w=(x-60)y=(x-60)(-x+120)
=-x2+180x-7200=-(x-90)2+900
∵a=-1<0 抛物线开口向下
又∵抛物线的对称轴是直线x=90
∴60≤x≤60(1+45%)=87时w随x的增大而增大
∴x=87时 w值最大 w最大值=891
∴该商场最大值为891元.
(3)把w=500代入w=-(x-90)2+900
500=-(x-90)2+900
解得x1=70 x2=110(不符合题意舍去)
∴70≤x≤87时 利润不低于500元.
点评 本题考查了二次函数的实际应用,用到的知识点是待定系数法求函数解析式,正确列出函数关系式是解决本题的关键,注意把不合题意得解舍去.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或2 | C. | -2或$\frac{1}{2}$ | D. | -$\frac{1}{2}$或2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
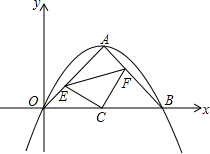 在平面直角坐标系中,抛物线y=ax2+bx+c经过坐标原点O、点A(2,2)和点B(4,0)三个点,连接OA、OB.得到△OAB,点E在OA边上从点O向点A匀速运动(其中点E不与点A、O重合),同时点F以相同的速度在AB边上从点A向点B运动.
在平面直角坐标系中,抛物线y=ax2+bx+c经过坐标原点O、点A(2,2)和点B(4,0)三个点,连接OA、OB.得到△OAB,点E在OA边上从点O向点A匀速运动(其中点E不与点A、O重合),同时点F以相同的速度在AB边上从点A向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
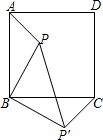 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.34×104 | B. | 13.4×104 | C. | 1.34×105 | D. | 0.134×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com