
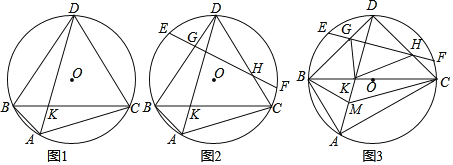
【题目】已知△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,交BC于点K,连接DB、DC.
(1)如图1,求证:DB=DC;
(2)如图2,点E、F在⊙O上,连接EF交DB、DC于点G、H,若DG=CH,求证:EG=FH;
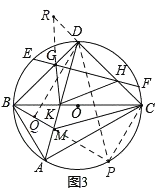
(3)如图3,在(2)的条件下,BC经过圆心O,且AD⊥EF,BM平分∠ABC交AD于点M,DK=![]() BM,连接GK、HK、CM,若△BDK与△CKM的面积差为1,求四边形DGKH的面积.
BM,连接GK、HK、CM,若△BDK与△CKM的面积差为1,求四边形DGKH的面积.
【答案】(1)见解析;(2)见解析;(3)DGKH的面积:4.
【解析】
(1)根据题意证明![]() 即可.
即可.
(2)连接OC、OD、OG、OH,作OM⊥GH.先证明△ODG≌△OCH,然后利用垂径定理可得结论.
(3)延长BM交圆O于P,连接CP、DP,作DQ⊥BM于Q,延长HD至R,使DR=DG,连接RG.先证DM=DC=DB,将△BDK与△CKM的面积差用BM表示从而求出BM的长,也就知道了DK的长,通过证明△DBK≌△HRG可知GH与DK相等,而四边形DGKH的面积就等于GH与DK乘积的一半.
解:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴![]() ,
,
∴DB=DC.
(2)如图2,连接OC、OD、OG、OH,作OM⊥GH.

则OD=OC,
∴∠OCH=∠ODH,
∵![]() ,
,
∴DO⊥BC,
∴∠ODG=∠ODH,
∴∠ODG=∠OCH,
在△ODG和△OCH中:
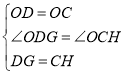
∴△ODG≌△OCH(SAS),
∴OG=OH,
∵OM⊥GH,
∴GM=MH,EM=FM,
∴EG=FH.
(3)如图3,延长BM交圆O于P,连接CP、DP,
作DQ⊥BM于Q,延长HD至R,使DR=DG,连接RG.
∵BC为直径,
∴∠BDC=∠BPC=90°,
∵DB=DC,
∴∠DBC=∠DCB=∠BPD=∠CPD=45°,
∵BM平分∠ABC,
![]() ,
,
∴∠PDM=∠PDC,
在△DPM和△DMC中:

∴△DPM≌△DMC(ASA),
∴DM=DC=DB,PC=PM,
∴∠MDQ=![]() ∠MDB,BQ=MQ=
∠MDB,BQ=MQ=![]() BM
BM
∴∠QDP=∠QDM+∠MDP=![]() ∠BDM+
∠BDM+![]() ∠MDC=
∠MDC=![]() ∠BDC=45°,
∠BDC=45°,
∴PQ=DQ,
∵DK⊥GH,
∴∠BDK=∠RHG,
∵RD=GD,∠GDR=90°,
∴∠GRH=45°=∠KBD,
又∵GD=CH,
∴RD=CH,
∴RH=CD=BD,
在△DBK和△HRG中:

∴△DBK≌△HRG(ASA),
∴HG=DK=![]() BM.
BM.
∵S△BDK﹣S△CKM=1,
∴S△BDM﹣S△CBM=1,
∴![]() ﹣
﹣![]() =
=![]() BM(DQ﹣CP)=
BM(DQ﹣CP)=![]() BM(PQ﹣PM)=
BM(PQ﹣PM)=![]() BM2=1.
BM2=1.
∴BM=2,
∴GH=DK=![]() BM=2
BM=2![]() ,
,
∴S四边形DGKH=![]() GHDK=4.
GHDK=4.


科目:初中数学 来源: 题型:
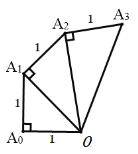
【题目】已知A0 A1= A1A2= A2A3…,图中的螺旋形由一系列直角三角形组成,则第n个三角形的面积为_________,周长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
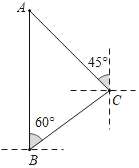
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大的方便了人们的出行.中国北斗导航已经全球组网,它已经走进了人们的日常生活.如图,某校组织学生到某地(用A表示)开展社会实践活动,车到达B地后,发现A地恰好在B地的正北方向,且距离B地10千米.导航显示车辆应沿北偏东60°方向行驶至C地,再沿北偏西45°方向行驶一段距离才能到达A地.求A、C两地间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
统计数据,并制作了如下统计表:
时间 |
|
|
|
|
男生 | 2 |
|
| 4 |
女生 | 1 | 5 | 9 | 3 |
分析数据:两组数据的极差、平均数、中位数、众数如表所示
极差 | 平均数 | 中位数 | 方差 | ||
男生 | 77 | 66.7 |
| 70 | 617.3 |
女生 |
| 69.7 | 70.5 |
| 547.2 |
(1)请将上面的表格补充完整:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人?
(3)体育老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持体育老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若cosC=![]() ,AC=6,求BF的长.
,AC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
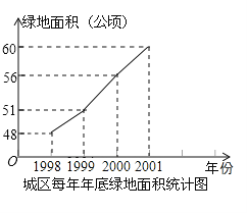
(1)根据图中所提供的信息,回答下列问题:2001年底的绿地面积为 公顷,比2000年底增加了 公顷;在1999年,2000年,2001年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2003年底使城区绿地总面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
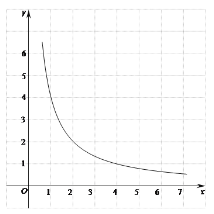
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
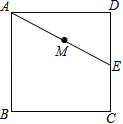
【题目】如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com