
分析 依据题意先用列表法展示所有等可能的结果数,再找出两次摸出的小球都是黑球的结果数,然后根据概率公式求解即可.
解答 解:列表如下:
| 黑1 | 黑2 | 黑3 | 白1 | 白2 | |
| 黑1 | 黑1黑1 | 黑1黑2 | 黑1黑3 | 黑1白1 | 黑1白2 |
| 黑2 | 黑2黑1 | 黑2黑2 | 黑2黑3 | 黑2白1 | 黑2白2 |
| 黑3 | 黑3黑1 | 黑3黑2 | 黑3黑3 | 黑3白1 | 黑3白2 |
| 白1 | 白1黑1 | 白1黑2 | 白1黑3 | 白1白1 | 白1白2 |
| 白2 | 白2黑1 | 白2黑2 | 白2黑3 | 白2白1 | 白2白2 |
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
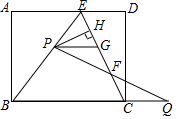 如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
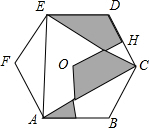 如图,点O是正六边形ABCDEF的中心,OG⊥AB,垂足为G,OH⊥CD,垂足为H,若在正六边形所在区域内随机选取一点,则该点落在阴影区域内的概率为$\frac{1}{3}$.
如图,点O是正六边形ABCDEF的中心,OG⊥AB,垂足为G,OH⊥CD,垂足为H,若在正六边形所在区域内随机选取一点,则该点落在阴影区域内的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
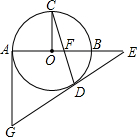 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
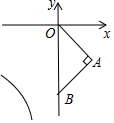 如图,平面直角坐标系中,等腰Rt△OAB沿x轴负方向向左平移后得到△O1A1B1,使点B的对应点B1落在双曲线y=$\frac{8}{x}$(x<0)上,若点B(0,-4),则线段AB扫过的面积是(平方单位)( )
如图,平面直角坐标系中,等腰Rt△OAB沿x轴负方向向左平移后得到△O1A1B1,使点B的对应点B1落在双曲线y=$\frac{8}{x}$(x<0)上,若点B(0,-4),则线段AB扫过的面积是(平方单位)( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
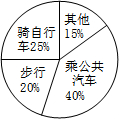 某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )
某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )| A. | 75人 | B. | 100人 | C. | 125人 | D. | 200人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
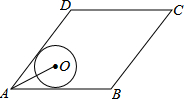 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com