
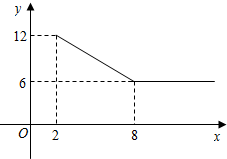
 某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.分析 (1)用待定系数法求得y与x的函数解析式,把x=5代入即可;
(2)根据“毛利润=销售总收入-经营总成本”计算即可求得结论;
(3)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入-经营总成本=wA+wB-3×20;
②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量.
解答 解:(1)设x,y的解析式为y=kx+b,
把x=2时,y=12,x=8时,y=6得:$\left\{\begin{array}{l}{2k+b=12}\\{8k+b=6}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=14}\end{array}\right.$,
∴y=-x+14(2≤x≤8),
∴x=5时,y=9,
答:A类杨梅的销售量为5吨时,它的平均销售价格是每吨9万元;
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则B类杨梅有6吨,
易得:WA=(10-3-1)×4=24(万元),
WA=6×(9-3)-(12+3×6)=6(万元),
∴W=24+6=30(万元),
答:此时经营这批杨梅所获得的毛利润w为30万元;
(3)设销售A类杨梅x吨,则销售B类杨梅(20-x)吨,
①当2≤x<8时,
wA=x(-x+14)-x=-x2+13x,
wB=9(20-x)-[12+3(20-x)]=108-6x,
∴w=wA+wB-3×20
=(-x2+13x)+(108-6x)-60
=-x2+7x+48;
当x≥8时,
wA=6x-x=5x,
wB=9(20-x)-[12+3(20-x)]=108-6x
∴w=wA+wB-3×20
=(5x)+(108-6x)-60
=-x+48,
∴w关于x的函数关系式为:
w=$\left\{\begin{array}{l}{{-x}^{2}+7x+48(2≤x<8)}\\{-x+48(x≥8)}\end{array}\right.$,
②当2≤x<8时,-x2+7x+48=30,解得x1=9,x2=-2,均不合题意,
当x≥8时,-x+48=30,解得x=18,
∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.
点评 本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | 5x=-1 | C. | x=3 | D. | 5x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
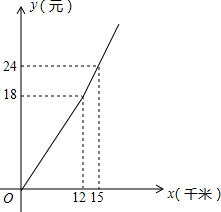 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )
随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )| A. | 32元 | B. | 34元 | C. | 36元 | D. | 40元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
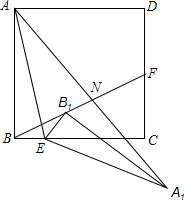 如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.
如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
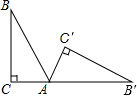 如图,在Rt△ABC中,∠B=30°,AC=1,将△ABC绕着点A按顺时针方向旋转到△AB′C′,使得B′落在CA的延长线上,则在旋转过程中,线段AB所扫过的面积为$\frac{4}{3}$π.
如图,在Rt△ABC中,∠B=30°,AC=1,将△ABC绕着点A按顺时针方向旋转到△AB′C′,使得B′落在CA的延长线上,则在旋转过程中,线段AB所扫过的面积为$\frac{4}{3}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com