
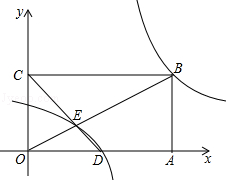
 我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).
我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).分析 (1)只需运用矩形的面积公式就可求出函数关系式,从而解决问题;
(2)可先求出直线OB和直线CD的解析式,求出它们的交点E的坐标,然后只需运用待定系数法就可解决问题;
(3)将坐标原点平移到点M的位置,构建新的坐标系,在新的坐标系中,分点P在点B的左边和右边两种情况讨论,只需先求出点P在新坐标系下的坐标,就可求出点P在原坐标系下的坐标
解答 解:(1)是广义反比例函数;
理由:由题意得:(2+x)(3+y)=8.
即3+y=$\frac{8}{x+2}$,
∴y=$\frac{8}{x+2}$-3=$\frac{-3x+2}{x+2}$.
根据定义,y=$\frac{-3x+2}{x+2}$是广义反比例函数.
(2)如图1,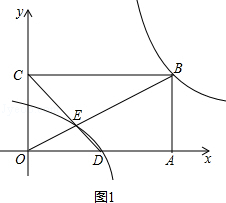
由题意得:B(6,3)、D(3,0),
设直线OB的解析式为y=mx,
则有6m=3,解得:m=$\frac{1}{2}$,
∴直线OB的解析式为y=$\frac{1}{2}$x.
设直线CD的解析式为y=kx+b,
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线CD的解析式为y=-x+3.
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-x+3}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴点E(2,1).
将点B(6,3)和E(2,1)代入y=$\frac{ax+k}{x-4}$得
$\left\{\begin{array}{l}{\frac{6a+k}{6-4}=3}\\{\frac{2a+k}{2-4}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-6}\end{array}\right.$,
∴广义反比例函数的表达式为y=$\frac{2x-6}{x-4}$.
(3)满足条件的点P的坐标为(2$\sqrt{5}$,$\sqrt{5}$+4)或(2$\sqrt{5}$+8,$\sqrt{5}$).
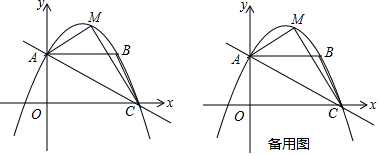
①若点P在点B的左边,如图2①,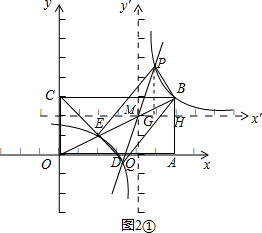
以点M为原点,构建如图2①所示的新坐标系,
在该坐标系下广义函数的解析式为y′=$\frac{2}{x'}$,点B的新坐标为(2,1).
∵直线PQ与双曲线y′=$\frac{2}{x'}$都是以点M为对称中心的中心对称图形,
∴MP=MQ.
∵MB=ME,
∴四边形BPEQ是平行四边形,
∴S?BPEQ=4S△BMP=16,
∴S△BMP=4.
过点P作PG⊥x′轴于G,过点B作BH⊥x′轴于H,
根据反比例函数比例系数的几何意义可得:
S△PGM=S△BHM=$\frac{1}{2}$×2=1,
∴S△BMP=S△PGM+S梯形BHGP-S△BHM=S梯形BHGP=4,
设点P在新坐标系中的坐标为(x′,$\frac{2}{x'}$),
则有S梯形BHGP=$\frac{1}{2}$(1+$\frac{2}{x'}$)•(2-x′)=4,
解得x1′=-4-2$\sqrt{5}$(舍去),x2′=-4+2$\sqrt{5}$,
当x=-4+2$\sqrt{5}$时,$\frac{2}{x'}$=$\frac{2}{-4+2\sqrt{5}}$=$\sqrt{5}$+2,
即点P在新坐标系中的坐标为(-4+2$\sqrt{5}$,$\sqrt{5}$+2),
∴点P在原坐标系中的坐标为(2$\sqrt{5}$,$\sqrt{5}$+4);
②若点P在点B的右边,如图2②,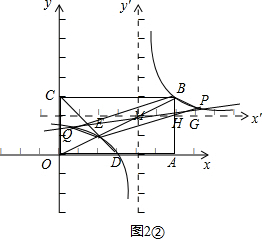
同理可得:点P在原坐标系中的坐标为(2$\sqrt{5}$+8,$\sqrt{5}$),
满足条件的点P的坐标为(2$\sqrt{5}$,$\sqrt{5}$+4),(2$\sqrt{5}$+8,$\sqrt{5}$)..
点评 此题是反比例函数综合题,属于新定义型,考查了运用待定系数法求函数的解析式,求两函数图象的交点、平行四边形的判定与性质、反比例函数比例系数的几何意义等知识,运用平移坐标轴法是解决第(3)小题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2009}$ | B. | $\frac{1}{2008}$ | C. | -$\frac{1}{2008}$ | D. | -$\frac{1}{2009}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6050 | B. | 6049 | C. | 6048 | D. | 6047 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x-2)2+1 | B. | y=3(x+2)2-1 | C. | y=3(x-2)2-1 | D. | y=3(x+2)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com