
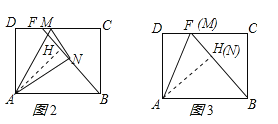
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.

【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=ADtan∠DAM=![]() 即可;
即可;
(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;
(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例![]() ,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
试题解析:(1)由折叠性质得:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB,∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=3×tan30°=![]() =
=![]() ;
;
(2)延长MN交AB延长线于点Q,如图1所示,∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折叠性质得:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ,设NQ=x,则AQ=MQ=1+x,∵∠ANM=90°,∴∠ANQ=90°,在Rt△ANQ中,由勾股定理得:![]() ,∴
,∴![]() ,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=
,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=![]() =
=![]() =
=![]() ANNQ=
ANNQ=![]() ;
;

(3)过点A作AH⊥BF于点H,如图2所示,∵四边形ABCD是矩形,∴AB∥DC,∴∠HBA=∠BFC,∵∠AHB=∠BCF=90°,∴△ABH∽△BFC,∴![]() ,∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:
,∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:
由折叠性质得:AD=AH,∵AD=BC,∴AH=BC,在△ABH和△BFC中,∵∠HBA=∠BFC,∠AHB=∠BCF,AH=BC,∴△ABH≌△BFC(AAS),∴CF=BH,由勾股定理得:BH![]() =
=![]() ,∴CF=
,∴CF=![]() ,∴DF的最大值=DC﹣CF=
,∴DF的最大值=DC﹣CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】从A地途径B地、C地,终点E地的长途汽车上原有乘客(6x+2y)人,在B地停靠时,上来(2x﹣y)人,在C地停靠时,上来了(2x+3y)人,又下去了(5x﹣2y)人.
(1)途中两次共上车多少人?
(2)到终点站E地时,车上共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0的条件是( )
A. a>0,△>0 B. a>0,△<0 C. a<0,△<0 D. a<0,△>0
查看答案和解析>>
科目:初中数学 来源: 题型:
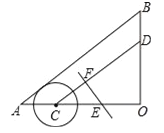
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了 s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com