
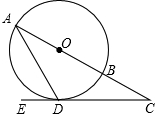
 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.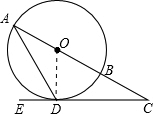 证明:(1)连接OD.
证明:(1)连接OD.| OD |
| CD |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线y=y=ax2-8ax+12a与x轴交A、B两点,P在y轴正半轴,PB与抛物线交于C,已知C是BP的中点,∠PBO=45°.
如图,抛物线y=y=ax2-8ax+12a与x轴交A、B两点,P在y轴正半轴,PB与抛物线交于C,已知C是BP的中点,∠PBO=45°.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、上午12时 | B、上午10时 |
| C、上午9时 | D、上午8时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com