
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,A、B、C是小正方形的顶点,求∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
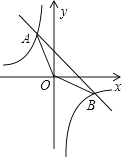
(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
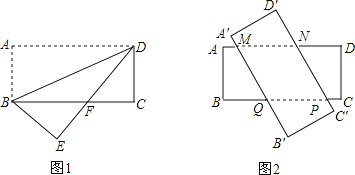
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=﹣ ![]() +|x|的图象与性质. 小军根据学习函数的经验,对函数y=﹣
+|x|的图象与性质. 小军根据学习函数的经验,对函数y=﹣ ![]() +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=﹣ ![]() +|x|的自变量x的取值范围是;
+|x|的自变量x的取值范围是;
(2)表是y与x的几组对应值
x | ﹣2 | ﹣1.9 | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | ﹣0.72 | ﹣1.41 | ﹣0.37 | 0 | 0.76 | 1.55 | … |
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察图象,函数的最小值是;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
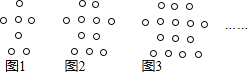
【题目】下列图形都是由同样大小的空心圆圈按照一定规律所组成的,其中图![]() 中一共有7个空心圆圈;图
中一共有7个空心圆圈;图![]() 中一共有11个空心圆圈;图
中一共有11个空心圆圈;图![]() 中一共有15个空心圆圈;
中一共有15个空心圆圈;![]()
![]() 图
图![]() 一共应有______个空心圆圈.
一共应有______个空心圆圈.
![]() 按此规律排列下去,猜想图
按此规律排列下去,猜想图![]() 中一共有多少个空心圆圈?用含n的代数式表示
中一共有多少个空心圆圈?用含n的代数式表示![]() 不用说理
不用说理![]() .
.
![]() 是否存在图
是否存在图![]() 中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com