
【题目】如图,以O为圆心的弧BD度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求![]() 的值;
的值;
(2)若OE与弧BD交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() +1.
+1.
【解析】分析:(1)、求出OB=BE,在Rt△OAD中,sin∠AOD=![]() ,代入求出即可;(2)、求出∠BOC=∠MOC,证△BOC≌△MOC,推出∠CMO=∠OBC=90°,根据切线的判定推出即可;(3)、求出CM=ME,MC=BC,求出BC=MC=ME=1,在Rt△MCE中,根据勾股定理求出CE=
,代入求出即可;(2)、求出∠BOC=∠MOC,证△BOC≌△MOC,推出∠CMO=∠OBC=90°,根据切线的判定推出即可;(3)、求出CM=ME,MC=BC,求出BC=MC=ME=1,在Rt△MCE中,根据勾股定理求出CE=![]() ,求出OB=
,求出OB=![]() +1,解直角三角形得出tan∠BCO=
+1,解直角三角形得出tan∠BCO=![]() +1,即可得出答案.
+1,即可得出答案.
详解:(1)∵EB⊥OB,∠BOE=45°,∴∠E=45°,∴∠E=∠BOE,∴OB=BE,
在Rt△OAD中,sin∠AOD=![]() ,∵OD=OB=BE,∴
,∵OD=OB=BE,∴![]() ;
;
(2)∵OC平分∠BOC,∴∠BOC=∠MOC,
在△BOC和△MOC中,OB=OM,∠BCO=∠MOC,OC=OC,∴△BOC≌△MOC(SAS),
∴∠CMO=∠OBC=90°,又∵CM过半径OM的外端,∴CM为⊙O的切线;
(3)由(1)(2)证明知∠E=45°,OB=BE,△BOC≌△MOC,CM⊥ME,
∵CM⊥OE,∠E=45°,∴∠MCE=∠E=45°,∴CM=ME,又∵△BOC≌△MOC,∴MC=BC,
∴BC=MC=ME=1,∵MC=ME=1,∴在Rt△MCE中,根据勾股定理,得CE=![]() ,
,
∴OB=BE=![]() +1,∵tan∠BCO=
+1,∵tan∠BCO=![]() ,OB=
,OB=![]() +1,BC=1,∴tan∠BCO=
+1,BC=1,∴tan∠BCO=![]() +1.
+1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,抛物线y=x2的顶点在直线AO上运动,与直线x=2交于点P,设平移后的抛物线顶点M的横坐标为m.
(1)如图1,若m=﹣1,求点P的坐标;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值;
(3)如图2,当线段BP最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.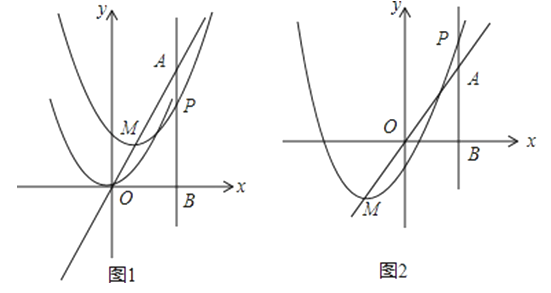
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?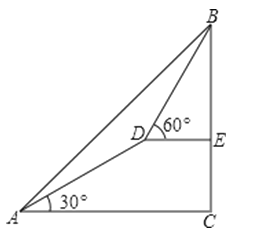
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_______海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A. 有理数就是正数和负数 B. 没有最小的有理数
C. 任何两个有理数一定可以进行加减乘除运算 D. 在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,负数共有
中,负数共有![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|-![]() +0.8|=____________;
+0.8|=____________;
(3)|![]() |=__________;
|=__________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-|-
|-|-![]() |-
|-![]() ×|-
×|-![]() |+
|+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )
A.(2014,0)
B.(2015,﹣1)
C.(2015,1)
D.(2016,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com