
【题目】如图1,在平面直角坐标系中,A(-2,0),B(0,6),C(6,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

【答案】(1)证明见解析;(2)32;(3)6.
【解析】
(1)根据四边形的内角和定理、直角三角形的性质证明;
(2)过点A作AF⊥BC于点F,作AE⊥CD的延长线于点E,作DG⊥x轴于点G,证明△ABF≌△ADE、△ABO≌△DAG,利用面积和可得四边形ABCD的面积;
(3)作EH⊥BC于点H,作EG⊥x轴于点G,根据角平分线的性质得到EH=EG,证明△EBH≌△EOG,得到EB=EO,根据等腰三角形的判定定理解出即可.
(1)如图1,在四边形ABCD中,∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°.
∵BC⊥CD,
∴∠BCD=90°.
∴∠BAD=90°.
∴∠BAC+∠CAD=90°.
又∵∠BAC+∠ABO=90°.
∴∠ABO=∠CAD.
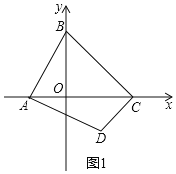
(2)如图2,过点A作AF⊥BC于点F,作AE⊥CD的延长线于点E,作DG⊥x轴于点G.
∵A(-2,0),B(0,6),C(6,0),
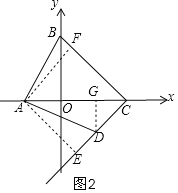
∴OA=2,OB=OC=6.
∴∠BCO=45°.
又∵BC⊥CD,
∴∠BCO=∠DCO=45°.
又∵AF⊥BC,AE⊥CD,
∴AF=AE,∠FAE=90°.
∴∠BAF=∠DAE,
∴△ABF≌△ADE.
∴AB=AD.
又∵∠AGD=∠BOA=90°,
∴△ABO≌△DAG.
∴DG=AO=2,AC=AO+OC=8.
∴S四边形ABCD=![]() AC(BO+DG)=
AC(BO+DG)=![]() =32.
=32.
(3)如图3,过点E作EH⊥BC于点H,作EG⊥x轴于点G,
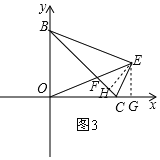
∵E点在∠BCO的邻补角的平分线上,
∴EH=EG.
又∵∠BCO=∠BEO=45°,
∴∠EBC=∠EOC.
∴△EBH≌△EOG.
∴EB=EO.
又∵∠BEO=45°,
∴∠EBO=∠EOB=67.5°.
∵∠OBC=45°,
∴∠BOE=∠BFO=67.5°.
∴BF=BO=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
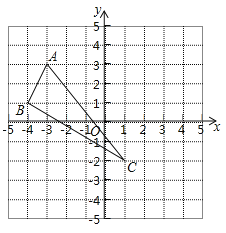
(2)直接写出A′、B′、C′三点的坐标:
A′(_____,______); B′(_____,______);
C′(_____,______).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
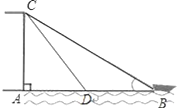
【题目】已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6![]() 米.
米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上周五购进某公司股票500股,每股30元.(星期六、星期日封盘,关闭交易)下表是本周内每日该股票比前一天的涨跌情况(单位:元)

星期一,星期二被墨水污染,只知道星期一比上周五上涨10%,星期二比星期一下跌10%.根据以上信息,请回答:
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)已知该股民购进股票时付了1.5‰的手续费,卖出时还要付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘时全部卖出该股票,他是赚钱还是亏本?赚或亏了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450克;第二天收集1号电池2节,5号电池3节,总质量为240克.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,他们随机抽取了该月某5天每天收集废电池的数量,如下表:
1号废电池数量/节 | 29 | 30 | 32 | 28 | 31 |
5号废电池数量/节 | 51 | 53 | 47 | 49 | 50 |
分别计算收集的两种废电池数量的样本平均数,并由此估算该月环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法是抽样调查还是全面调查,你认为这种方法合理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com