
【题目】△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.
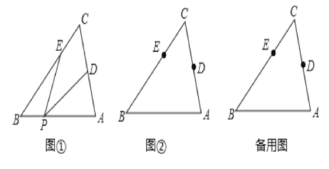
(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=___;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
【答案】(1)90°;(2)①见解析,②60°α;(3)60°+α或60°α或60°;
【解析】
(1)连接PC,由三角形的外角性质即可得出结论;
(2)①根据题意画出图形即可;
②由三角形的外角性质即可得出结论;
(3)分三种情况讨论,由三角形的外角性质即可得出结论.
;(1)∠PEB+∠PDA=90;理由如下;
连接PC,如图1所示
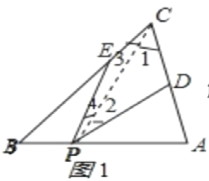
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+30°=90
故答案为:90°;
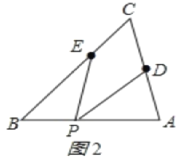
(2)①如图2所示;
②连接PC,如图3所示:
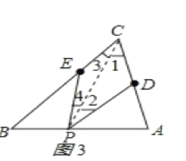
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角,
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+α;
∴∠PEB+∠PDA=60°+α;
(3)分三种情况:
①如图4所示:
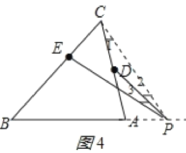
连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2+∠3,∠PDA=∠1+∠2
∴∠PEB∠PDA=∠ACB+∠3=60°+α;
②如图5所示:连接PC,
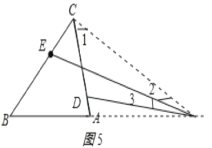
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2+∠3
∴∠PEB∠PDA=∠ACB∠3=60°α;
③如图6所示:P、D. E在同一条直线上,连接PC,
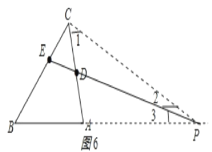
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2,
∴∠PEB∠PDA=∠ACB=60°;
综上所述:如果点P在线段BA的延长线上运动,
∠PEB与∠PDA之间的数量关系是60°+α或60°α或60°;
故答案为:60°+α或60°α或60°.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,点D、E分别在边AB、AC上,点F在CD上.
(1)若∠AED=∠ACB, ∠DEF= ∠B,求证:EF//AB;
(2)若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形 BDEF的面积为6,试求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点分别是A(2,0)、B(0,4)、C(-3,0),把△ABC沿x轴向右平移4个单位,得到△A1B1C1.
(1)在图中以黑点为原点建立平面直角坐标系,画出△ABC和△A1B1C1;
(2)写出A1、B1、C1各点的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 度;
(2)求∠CAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com