练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．（-2$\sqrt{5}$）2=20．

    分析 直接利用积的乘方运算法则化简求出即可．

    解答 解：（-2$\sqrt{5}$）2=（-2）2×（$\sqrt{5}$）2=20．
    故答案为：20．

    点评 此题主要考查了二次根式的乘法运算，正确应用积的乘方运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

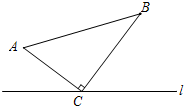    4．如图，△ABC中，∠ACB=90°，AC=8cm，BC=15cm，点M从A点出发沿A→C→B路径向终点运动，终点为B点，点N从B点出发沿B→C→A路径向终点运动，终点为A点，点M和N分别以每秒2m和3cm的运动速度同时开始运动，两点都要到达相应的终点时才能停止运动，分别过M和N作ME⊥l于E，NF⊥l于F．设运动时间为t秒，要使以点M，E，C为顶点的三角形与以点N，F，C为顶点的三角形全等，则t的值为$\frac{23}{5}$或7或8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

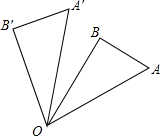    6．如图，在直角△OAB中，∠AOB=30°，OA=2，将△OAB绕点O逆时针旋转n°得到△OA′B′，则∠A′OB、OA′大小分别为（　　）
    A．n°，1B．n°，2C．n°-30°，1D．n°-30°，2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知抛物线y=x2+bx+c与x轴交于点A、B两点（A点在B点左侧），与y轴交于点C（0，-3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
    （1）求出抛物线的函数表达式；
    （2）设点E时抛物线上一点，且S△ABE=$\frac{5}{3}$S△ABC，求tan∠ECO的值；
    （3）点P在抛物线上，点Q在抛物线对称轴上，若以B、C、P、Q为顶点的四边形是平行四边形，求点P坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．先化简，再求值：$\frac{3-x}{x-2}$÷（x+2-$\frac{5}{x-2}$），其中x=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环．则射中环数的中位数是8，众数是8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

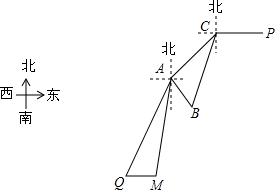    7．南沙群岛自古以来都是中国领土，如图，点A、B、C分别表示南沙群岛的三个小岛，岛C在岛A的北偏东45°方向，岛B在岛C的南偏西15°方向上，岛B在岛A的南偏东30°方向，且岛A、岛B两岛的距离为3海里．
    （1）求岛A、岛C间的距离；
    （2）我国南海某雷达观测站发现一艘不明国籍舰艇正从岛C正东10海里的点P处以20海里/小时的速度接近岛A，其航线为P→C→A（直线行进），而我某海警船正位于岛A西偏南60°方向12海里的点Q处，收到上级命令迅速前往A岛，其航线为先向正东航行8海里至点M处，再折向点A直线航行，航速为30海里/小时，问海警船能否先于不明国籍舰艇到达岛A？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知关于x的方程（x-1）[（k-1）x+（k-3）]=0（k是常数），则下列说法中正确的是（　　）
    A．方程一定有两个不相等的实数根B．方程一定有两个实数根
    C．当k取某些值时，方程没有实数根D．方程一定有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．2014年6月，甲、乙、丙、丁四位备战南京青奥会射击选手在一次训练比赛中，这四位选手各射击10次，每人的平均成绩都是9.5环，方差如下表：
    选手甲乙丙丁
    方差（环2）0.350.0180.220.055
    则在这次训练比赛中，这四位选手发挥最稳定的是（　　）
    A．甲B．乙C．丙D．丁

    查看答案和解析>>

    同步练习册答案