»γΆΦΘ§“―÷ΣΘΚΓςABCΈΣ±Ώ≥Λ «
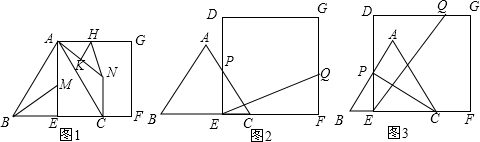
4ΒΡΒ»±Ώ»ΐΫ«–ΈΘ§ΥΡ±Ώ–ΈDEFGΈΣ±Ώ≥Λ «6ΒΡ’ΐΖΫ–ΈΘ°œ÷ΫΪΒ»±ΏΓςABCΚΆ’ΐΖΫ–ΈDEFGΑ¥»γΆΦ1ΒΡΖΫ ΫΑΎΖ≈Θ§ ΙΒψC”κΒψE÷ΊΚœΘ§ΒψBΓΔCΘ®EΘ©ΓΔF‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§ΓςABC¥”ΆΦ1ΒΡΈΜ÷Ο≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊEFΖΫœρœρ”“‘»ΥΌ‘ΥΕ·Θ§Β±ΒψC”κΒψF÷ΊΚœ ±‘ίΆΘ‘ΥΕ·Θ§…ηΓςABCΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ®tΓί0Θ©Θ°

Θ®1Θ©‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Θ§…ηΒ»±ΏΓςABCΚΆ’ΐΖΫ–ΈDEFG÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§«κ÷±Ϋ”–¥≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
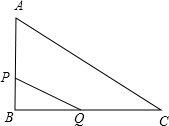
Θ®2Θ©»γΆΦ2Θ§Β±ΒψA”κΒψD÷ΊΚœ ±Θ§ΉςΓœABEΒΡΫ«ΤΫΖ÷œΏBMΫΜAE”ΎMΒψΘ§ΫΪΓςABM»ΤΒψAΡφ ±’κ–ΐΉΣΘ§ Ι±ΏAB”κ±ΏAC÷ΊΚœΘ§ΒΟΒΫΓςACNΘ°‘ΎœΏΕΈAG…œ «Ζώ¥φ‘ΎHΒψΘ§ ΙΒΟΓςANHΈΣΒ»―ϋ»ΐΫ«–ΈΘ°»γΙϊ¥φ‘ΎΘ§«κ«σ≥ωœΏΕΈEHΒΡ≥ΛΕ»ΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©»γΆΦ3Θ§»τΥΡ±Ώ–ΈDEFGΈΣ±Ώ≥ΛΈΣ
4ΒΡ’ΐΖΫ–ΈΘ§ΓςABCΒΡ“ΤΕ·ΥΌΕ»ΈΣΟΩΟκ
ΗωΒΞΈΜ≥ΛΕ»Θ§Τδ”ύΧθΦΰ±Θ≥÷≤Μ±δΘ°ΓςABCΩΣ Φ“ΤΕ·ΒΡΆ§ ±Θ§QΒψ¥”FΒψΩΣ ΦΘ§―Ί’έœΏFG-GD“‘ΟΩΟκ
2ΗωΒΞΈΜ≥ΛΕ»ΩΣ Φ“ΤΕ·Θ§ΓςABCΆΘ÷Ι‘ΥΕ· ±Θ§QΒψ“≤ΆΘ÷Ι‘ΥΕ·Θ°…η‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§DEΫΜ’έœΏBA-AC”ΎPΒψΘ§‘ρ «Ζώ¥φ‘ΎtΒΡ÷ΒΘ§ ΙΒΟPCΓΆEQΘ§»τ¥φ‘ΎΘ§«κ«σ≥ωtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°






 »γΆΦΘ§“―÷ΣΘΚΓςABC÷–Θ§Γœ1=Γœ2Θ§«“AE=ADΘ§BEΚΆCDœύΫΜ”ΎFΘ°«σ÷ΛΘΚBF=CFΘ°
»γΆΦΘ§“―÷ΣΘΚΓςABC÷–Θ§Γœ1=Γœ2Θ§«“AE=ADΘ§BEΚΆCDœύΫΜ”ΎFΘ°«σ÷ΛΘΚBF=CFΘ° »γΆΦΘ§“―÷ΣΘΚΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§DΓΔFΖ÷±πΈΣ…δœΏBCΓΔ…δœΏAB±Ώ…œΒΡΒψΘ§BD=AFΘ§“‘ADΈΣ±ΏΉςΒ»±ΏΓςADEΘ°
»γΆΦΘ§“―÷ΣΘΚΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§DΓΔFΖ÷±πΈΣ…δœΏBCΓΔ…δœΏAB±Ώ…œΒΡΒψΘ§BD=AFΘ§“‘ADΈΣ±ΏΉςΒ»±ΏΓςADEΘ° »γΆΦΘ§“―÷Σ‘ΎΓςABC÷–Θ§AB=ACΘ§ΓœA=36ΓψΘ§BDΈΣΓœABCΒΡΤΫΖ÷œΏΘ§‘ρ
»γΆΦΘ§“―÷Σ‘ΎΓςABC÷–Θ§AB=ACΘ§ΓœA=36ΓψΘ§BDΈΣΓœABCΒΡΤΫΖ÷œΏΘ§‘ρ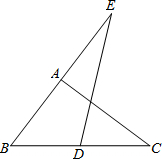 »γΆΦΘ§“―÷Σ‘ΎΓςABC÷–Θ§D «±ΏBCΒΡ÷–ΒψΘ§ΒψE‘Ύ±ΏBAΒΡ―”≥ΛœΏ…œΘ§AE=ABΘ§
»γΆΦΘ§“―÷Σ‘ΎΓςABC÷–Θ§D «±ΏBCΒΡ÷–ΒψΘ§ΒψE‘Ύ±ΏBAΒΡ―”≥ΛœΏ…œΘ§AE=ABΘ§