
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
| 丙 | 50 | 60 | 85 |
分析 (1)根据商品知识分别赋权2、3、5和各自的得分,分别进行计算,然后进行比较即可;
(2)根据加权平均数的计算公式分别列出算式,再进行计算即可.
解答 解:(1)甲成绩:$\frac{70×2+50×3+80×5}{2+3+5}$=69(分),
乙成绩:$\frac{90×2+75×3+45×5}{2+3+5}$=63(分),
丙成绩:$\frac{50×2+60×3+85×5}{2+3+5}$=70.5(分),
因此丙成绩最高,应被录取.
(2)甲成绩:70×50%+50×30%+80×20%=66(分),
乙成绩:90×50%+75×30%+45×20%=76.5(分),
丙成绩:50×50%+60×30%+85×20%=60(分),
因此乙成绩最高,应被录取.
点评 此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键,是一道基础题.


科目:初中数学 来源: 题型:解答题
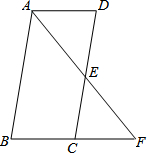 如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com