
 甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:分析 ①根据图象可知:甲队挖掘600米,需要6天,故可求得甲队的挖掘速度;
②由函数图象可知乙队开挖两天后,用4天时间,挖掘200米;
③求得乙队完成任务需要的天数即可;
④由甲的工作效率就可以求出2天时的工作量为200米,乙队是300米.6天时甲队是600米,乙队是500米得出300-200=600-500=100米.
解答 解:①600÷6=100,故①正确;
②(500-300)÷(6-2)=200÷4=50,故②正确;
③(600-300)÷50=6天,所以乙队共需要8天完成任务,甲队需要6天完成任务,故③正确.
④当x=2时,甲队完成的工作量为:2×100=200米,
乙队完成的工作量为:300米.
当x=6时,甲队完成的工作量为600米,乙队完成的工作量为500米.
∵300-200=600-500=100,
∴当x=2或6时,甲乙两队所挖管道长度都相差100米.故正确.
故答案为①②③④.
点评 本题主要考查的是一次函数的应用,根据函数图象求得两队的挖掘速度是解题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x-1=x+5移项得2x+x=5+1 | B. | $\frac{x}{2}$+$\frac{x}{3}$=1去分母得3x+2x=1 | ||
| C. | (x+2)-2(x-1)=0去括号得x+2-2x+2=0 | D. | -4x=2系数化为“1”得x=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
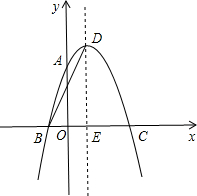 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
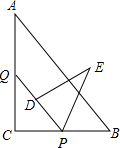 如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com