
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得Cn.若P(2014,m)在第n段抛物线Cn上,则m=-2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得Cn.若P(2014,m)在第n段抛物线Cn上,则m=-2. 分析 根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,进而求出m的值.
解答 解:∵一段抛物线:y=-x(x-3)(0≤x≤3),
∴图象与x轴交点坐标为:(0,0),(3,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得Cn.
∴C672的解析式与x轴的交点坐标为(2013,0),(2016,0),且图象在x轴下方,
∴C672的解析式为:y672=(x-2013)(x-2016),
当x=2014时,m=(2014-2013)×(2014-2016)=-2.
故答案为:-2.
点评 此题主要考查了二次函数的平移规律,根据已知得出二次函数旋转后解析式是解题关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价(元) | x |
| 销售量y(件) | -10x+1000 |
| 销售玩具获得利润w(元) | -10x2+1200x-20000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
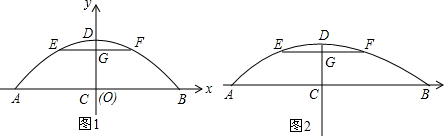
 二次函数的图象如图所示,下列结论:①a<0;②-$\frac{b}{2a}$=1;③b2-4ac<0;④当x>1时,y随x的增大而减小;⑤.当-1<x<3时,y<0,其中正确的是②⑤.(只填序号)
二次函数的图象如图所示,下列结论:①a<0;②-$\frac{b}{2a}$=1;③b2-4ac<0;④当x>1时,y随x的增大而减小;⑤.当-1<x<3时,y<0,其中正确的是②⑤.(只填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
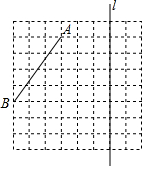 如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.
如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( )
如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三条中线的交点 | B. | 三条高线的交点 | ||
| C. | 三条角平分线的交点 | D. | 三边垂直平分线的交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com